Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A P. 4443. feladat (2012. április)

P. 4443. Az ábrán látható $\ell$ átmérőjű drótkeretben $\sigma$ felületi feszültségű szappanhártyát hoztunk létre. A P és Q pontokat $\ell$ hosszúságú, E Young-modulusú, A keresztmetszetű, feszítetlen hajszál köti össze.

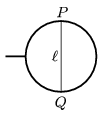
Mennyivel nyúlik meg a hajszál, ha a jobb oldali hártyát egy forró fémtűvel átszúrjuk?

(A hajszál végei rögzítettek és a súlya elhanyagolható. Kis szögekre használhatjuk a sin $\alpha$ $\approx$ $\alpha$ - $\alpha$ ³/6 közelítést.)

Varga István (1952--2007) feladata

(6 pont)

A beküldési határidő 2012. május 10-én LEJÁRT.

Megoldásvázlat. A megnyúlás

$\Delta \ell=\frac{\ell}{6}\left(\frac{6\ell\sigma}{EA} \right)^{\frac{2}{3}}.$

Statisztika:

13 dolgozat érkezett.

6 pontot kapott: Szabó 928 Attila.

5 pontot kapott: Barta Szilveszter Marcell, Czipó Bence, Juhász Péter, Koncz Gabriella, Papp Roland, Sárvári Péter, Szélig Áron, Trócsányi Péter, Vajda Balázs.

4 pontot kapott: 3 versenyző.

A KöMaL 2012. áprilisi fizika feladatai

13 dolgozat érkezett.
6 pontot kapott:	Szabó 928 Attila.
5 pontot kapott:	Barta Szilveszter Marcell, Czipó Bence, Juhász Péter, Koncz Gabriella, Papp Roland, Sárvári Péter, Szélig Áron, Trócsányi Péter, Vajda Balázs.
4 pontot kapott:	3 versenyző.