 |
A P. 4469. feladat (2012. október) |
P. 4469. Azonos pontban felfüggesztett, azonos hosszúságú fonalakon lógó, m1 és m2 tömegű testeket feszes fonalakkal a függőleges iránytól jobbra és balra azonos szöggel kitérítünk, majd egy adott pillanatban egyszerre magukra hagyjuk őket. A testek mozgásuk során tökéletesen rugalmatlanul ütköznek. A testek helyzetét a pálya legmélyebb pontján átmenő vízszintes sík feletti magassággal jellemezzük. (A közegellenállás elhanyagolható.) Adjuk meg a rugalmatlan ütközés utáni legnagyobb magasság és a kezdeti magasság hányadosát!
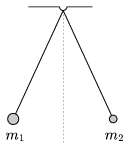
Közli: Kotek László, Pécs
(4 pont)
A beküldési határidő 2012. november 12-én LEJÁRT.
Megoldásvázlat.
\(\displaystyle h_1=\left( \frac{m_1-m_2}{m_1+m_2} \right)^2 h_0.\)
Statisztika:
167 dolgozat érkezett. 4 pontot kapott: 142 versenyző. 3 pontot kapott: 17 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2012. októberi fizika feladatai
