 |
A P. 4500. feladat (2013. január) |
P. 4500. Egy kis gyöngy az ábrán látható két pályán csúszhat le az A pontból a B pontba. A pályák függőleges síkban fekvő körívek, melyek szimmetrikusak az A és B pontokon átmenő, a vízszintessel 45o-os szöget bezáró egyenesre.
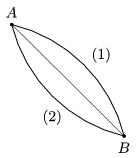
a) Melyik pályán ér le hamarabb a gyöngy, és mit mondhatunk a végsebességekről, ha nincs súrlódás?
b) Mit állíthatunk a végsebességekről akkor, ha a súrlódás nem hanyagolható el, és a súrlódási együttható mindkét pályán ugyanakkora?
Közli: Sütt Dezső, Budapest
(4 pont)
A beküldési határidő 2013. február 11-én LEJÁRT.
Megoldásvázlat. \(\displaystyle a)\) Súrlódásmentes esetben a (2)-es pályán ér le hamarabb, de a végsebesség mindkét pályán ugyanakkora.
\(\displaystyle b)\) Ha mindkét test végig tud csúszni a pályáján, akkor az (1)-es pályán haladó végsebessége lesz nagyobb. (Elképzelhető azonban az is, hogy az (1)-es pályán el sem indul a gyöngy, illetve a (2)-es pályán haladó esetleg útközben megállhat.)
Statisztika:
74 dolgozat érkezett. 4 pontot kapott: Antalicz Balázs, Balogh Menyhért, Emri Tamás, Fekete Panna, Filep Gábor, Juhász Péter, Kaprinai Balázs, Putti Krisztián, Sági Olivér, Soós Tamás Sándor, Tóth Bálint. 3 pontot kapott: Bősze Zsófia, Fábián Kristóf, Hajós Mátyás, Huszár Emese, Mezősi Máté, Nagy Gergely, Nemes György, Wiandt Péter, Zsiros Ádám. 2 pontot kapott: 20 versenyző. 1 pontot kapott: 23 versenyző. 0 pontot kapott: 11 versenyző.
A KöMaL 2013. januári fizika feladatai
