 |
A P. 4501. feladat (2013. január) |
P. 4501. Lefelé fordított U alakú, keskeny, kicsi, rögzített csőből egy 
hosszúságú kötél lóg ki az ábra szerint. Kezdetben a kötél mindkét oldalon /2 hosszúságú. Itt labilis egyensúlyi helyzetben van, minthogy a súrlódás elhanyagolható.
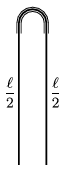
a) Ha a kötél valamelyik oldalra csúszni kezd, mekkora lesz a sebessége, mire kiegyenesedik?
b) Mekkora a kötél sebessége akkor, amikor a kötél pillanatnyi tömegközéppontja éppen a felfelé csúszó kötéldarab végével van azonos magasságban?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
A beküldési határidő 2013. február 11-én LEJÁRT.
Megoldásvázlat.
\(\displaystyle v_a=\sqrt{\frac{g\ell}{2}}\approx 0{,}71\sqrt{g\ell};\)
\(\displaystyle v_b=\sqrt{\left(\frac{3}{2}-\sqrt{2}\right)g\ell}\approx0{,}29\sqrt{g\ell}.\)
Statisztika:
97 dolgozat érkezett. 4 pontot kapott: Antalicz Balázs, Balogh Menyhért, Barta Szilveszter Marcell, Berta Dénes, Bingler Arnold, Bugár 123 Dávid, Csáky Pál, Csathó Botond, Dávid Bence, Essig-Kacsó Attila, Fábián Kristóf, Farkas Tamás, Fehér Zsombor, Fekete Panna, Fonyó Viktória, Forrai Botond, Holczer András, Horváth János, Janzer Barnabás, Jenei Márk, Juhász Péter, Kollarics Sándor, Krokos Ádám László, Maga Balázs, Medek Ákos, Olexó Tünde, Olosz Balázs, Öreg Botond, Sal Kristóf, Sárvári Péter, Seress Dániel, Sztilkovics Milán, Tatár Dániel, Tegzes Tamás, Ürge László, Vajda Balázs, Váli Tamás, Varga Blanka, Zsiros Ádám. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 21 versenyző. 1 pontot kapott: 17 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2013. januári fizika feladatai