 |
A P. 4587. feladat (2013. december) |
P. 4587. Egy függőleges, rögzített rúdon fel-le mozoghat egy pontszerűnek tekinthető m tömegű test. A test közepén függőleges furat található, ezen megy át a rúd, ami a test számára súrlódásmentes mozgást biztosít. A testhez két könnyű, vékony fonál csatlakozik, melyek kezdetben  =45o-os szöget zárnak be a függőlegessel. A fonalak azonos magasságban lévő, rögzített csigákon haladnak át, a végükre M=1 kg tömegű testeket rögzítettünk. A rendszert nyugalmi állapotból indítjuk el.
=45o-os szöget zárnak be a függőlegessel. A fonalak azonos magasságban lévő, rögzített csigákon haladnak át, a végükre M=1 kg tömegű testeket rögzítettünk. A rendszert nyugalmi állapotból indítjuk el.
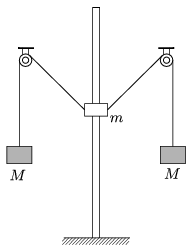
a) Mekkora a rúdon mozgó test m tömege, ha az elengedést követően éppen olyan magasságban áll meg, amikor a hozzá rögzített fonalak vízszintes helyzetűek?
b) Mekkora gyorsulással indul el visszafelé a m tömegű test, és mekkora gyorsulással indulnak el visszafelé a M tömegű testek?
Közli: Honyek Gyula, Budapest
(4 pont)
A beküldési határidő 2014. január 10-én LEJÁRT.
Megoldásvázlat. \(\displaystyle a)\) \(\displaystyle m=2M(\sqrt{2}-1)=\)0,82 kg.
\(\displaystyle b)\) A \(\displaystyle m\) tömegű test \(\displaystyle g\) gyorsulással kezd el esni, a \(\displaystyle M\) tömegű testek gyorsulása ugyanebben a pillanatban nulla.
Statisztika:
67 dolgozat érkezett. 4 pontot kapott: Antalicz Balázs, Bartók Imre, Béda Ármin, Berczi Benjámin, Bereczki Zoltán, Csáky Pál, Demeter Dániel, Di Giovanni Márk, Dombai Tamás, Farkas Tamás, Fehér Zsombor, Fekete Panna, Gróf Tamás, Holczer András, Horváth András Levente, Iván Balázs, Janzer Barnabás, Juhász Péter, Kacz Dániel, Kaposvári Péter, Kasza Bence, Kovács Péter Tamás, Mándoki László, Marosvári Kristóf, Nagy Zsolt, Németh 017 András, Németh Flóra Boróka, Olosz Balázs, Rózsa Tibor, Seress Dániel, Szántó Benedek, Szász Norbert Csaba, Szathmári Balázs, Szentivánszki Soma , Tanner Martin, Varju Ákos, Verasztó Ádám, Zarándy Álmos. 3 pontot kapott: Balogh Menyhért, Berta Dénes, Biri Eszter Daniela, Dinev Georgi, Kácsor Szabolcs, Koncz Imre, Kormányos Hanna Rebeka, Krokos Ádám László, Pázmán Zalán, Stein Ármin, Turi Soma, Wiandt Péter. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2013. decemberi fizika feladatai
