A P. 4630. feladat (2014. április)

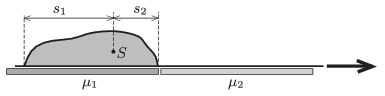
P. 4630. Egy zsáknyi homok vízszintes felületen egy könnyű szőnyegen fekszik. Az \(\displaystyle M\) tömegű zsákot a szőnyeg segítségével lassan át akarjuk húzni egy viszonylag sima felületről egy érdesebb felületre. Mennyi munkát kell végeznünk, ha a felületek és a szőnyeg közötti súrlódási együttható \(\displaystyle \mu_1\), illetve \(\displaystyle \mu_2\)? A zsák súlya nem egyenletesen oszlik el a szőnyegen, de tudjuk, hogy a tömegközéppontja a széleitől \(\displaystyle s_1\), illetve \(\displaystyle s_2\) távolságban van. (Lásd még a P. 4554. megoldott feladatot lapunk 237. oldalán!)

Közli: Gnädig Péter, Vácduka

(5 pont)

A beküldési határidő 2014. május 12-én LEJÁRT.

Megoldásvázlat. \(\displaystyle W=Mg\left(s_2\mu_1+s_1\mu_2\right).\)

Statisztika:

39 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Fehér Zsombor, Forrai Botond, Holczer András, Horicsányi Attila, Janzer Barnabás, Juhász Péter, Kaposvári Péter, Lőrincz Zoltán, Olosz Balázs, Öreg Botond, Rózsa Tibor, Sal Kristóf, Seress Dániel.
3 pontot kapott:	16 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2014. áprilisi fizika feladatai