A P. 4675. feladat (2014. november)

P. 4675. Egy \(\displaystyle M=1000\) kg tömegű, homogén tömegeloszlásúnak tekinthető páncélszekrény kocka alakú, magassága \(\displaystyle \ell=1\) méter. A páncélszekrény 4 kicsi lábon áll egy olyan garázs ajtajánál, ahol a páncélszekrény és az érdes kőburkolat között a súrlódási együttható \(\displaystyle \mu_1=0{,}9\). A garázson kívül a talaj már nem ennyire érdes, ott a súrlódási együttható \(\displaystyle \mu_2=0{,}5\).

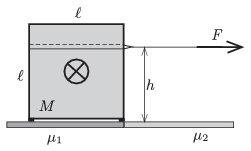
Egy szállítóbrigád \(\displaystyle h\) magasságban kifeszített vízszintes drótkötél és egy motoros csörlő segítségével ki akarja húzni a páncélszekrényt a garázsból. A csörlő (amelyet egy erős oszlophoz akarnak rögzíteni) maximálisan 6000 N erő kifejtésére képes. A brigád (fizikából) legjobban képzett tagja azt állítja, hogy erősebb csörlőre lenne szükség, mert a páncélszekrény súlyát az átlagos súrlódási tényezővel megszorozva 7000 N adódik, és ez még akkor is meghaladja a csörlő teherbírását, ha induláskor némi izomerő segítségével sikerülne átcsúsztatni a páncélszekrény 2 első lábát a kevésbé érdes felületre.

Igaza van-e a brigád ,,fizikusának''?

Közli: Gnädig Péter, Vácduka

(5 pont)

A beküldési határidő 2014. december 10-én LEJÁRT.

Megoldás: A mozgatáshoz szükséges kötélerő

\(\displaystyle F=Mg\frac{\mu_1+\mu_2}{2}\cdot \frac{1}{1+(h/\ell)(\mu_1-\mu_2)}\approx10 000~{\rm N}\cdot 0{,}7\,\frac{1}{1+0{,}4(h/\ell)}.\)

Mivel \(\displaystyle h\le \ell\), \(\displaystyle F\ge 5000\) N, és a határeset jól megközelíthető, ha a kötelet majdnem a szekrény legtetejéhez rögzítik, a brigád ,,fizikusa'' tévedett.

Statisztika:

60 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bencsik Bálint, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Büki Máté, Csathó Botond, Csorba Benjámin, Fehér Balázs, Fekete Balázs Attila, Fekete Gábor, Fekete Panna, Forrai Botond, Fülöp Erik, Gróf Tamás, Holczer András, Jeges Viktor, Juhász 326 Dániel, Kaposvári Péter, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Körtefái Dóra, Molnár 157 Marcell, Molnár Elizabet, Németh 017 András, Németh Flóra Boróka, Olosz Balázs, Orosz Bálint, Páhoki Tamás, Plaszkó Noel, Radnai Bálint, Rózsa Tibor, Sal Kristóf, Szántó Benedek, Szász Norbert Csaba, Szentivánszki Soma , Szirbik Bence, Tompa Tamás Lajos, Varga-Umbrich Eszter, Varju Ákos, Wiandt Péter.
4 pontot kapott:	Nagy Kartal, Südi István, Zarándy Álmos.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	4 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2014. novemberi fizika feladatai