A P. 4681. feladat (2014. november)

P. 4681. Az ábrán látható, \(\displaystyle 3N\) darab egyforma ellenállásból álló láncból zárt szalagot készíthetünk kétféle módon:

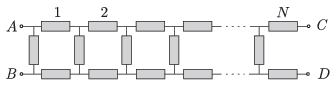
\(\displaystyle a)\) az \(\displaystyle A\) és \(\displaystyle C\), illetve a \(\displaystyle B\) és \(\displaystyle D\) kivezetéseket páronként összekötjük;

\(\displaystyle b)\) az \(\displaystyle A\) és \(\displaystyle D\), illetve a \(\displaystyle B\) és \(\displaystyle C\) kivezetéseket páronként összekötjük (Möbius-szalag).

Melyik esetben lesz nagyobb az eredő ellenállás a szalag \(\displaystyle A\) és \(\displaystyle B\) pontja között?

Közli: Vigh Máté, Budapest

(6 pont)

A beküldési határidő 2014. december 10-én LEJÁRT.

Megoldás: Az ábra alkalmas átrajzolásával (az ekvipotenciális pontok rövidrezárásával, vagy a közöttük levő ellenállás eltávolításával) belátható, hogy mind páros, mind páratlan \(\displaystyle N\)-ekre \(\displaystyle R_\text{Möbius}<R_\text{henger}\).

Statisztika:

13 dolgozat érkezett.
6 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Csathó Botond, Fekete Panna, Forrai Botond, Holczer András, Kaposvári Péter, Sal Kristóf.
4 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2014. novemberi fizika feladatai