 |
A P. 4788. feladat (2015. december) |
P. 4788. Egy \(\displaystyle a=2\) cm oldalú szabályos hatszög minden második csúcsán át, a hatszög síkjára merőlegesen, hosszú, egyenes vezetőkben \(\displaystyle I=10~\)A nagyságú áram folyik, kettőben felfelé, egyben pedig lefelé.
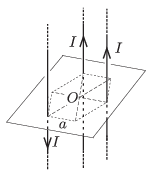
\(\displaystyle a)\) Mekkora és milyen irányú a mágneses indukció a hatszög középpontjában?
\(\displaystyle b)\) Mekkora nagyságú és milyen irányú erő hat az egyes vezetők \(\displaystyle \ell=1\) m hosszúságú darabjára?
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2016. január 11-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Mindegyik áram (külön-külön) a vezetéktől \(\displaystyle a\) távolságban
\(\displaystyle B_0=\mu_0\frac{I}{2\pi a}=0{,}1~\rm mT\)
nagyságú mágneses indukciót hoz létre a hatszög középpontjában. Az eredő mágneses indukció a három áram járulékának vektori összege. Ha mindegyik áram ugyanolyan irányban folyna, akkor az eredő mágneses indukció az \(\displaystyle O\) pontban (a szimmetria miatt) nulla lenne. Eszerint a felfelé folyó áramok eredő mágneses indukciója éppen \(\displaystyle (-1)\)-szerese a lefelé folyó áram járulékának. A három áramvezető eredő mágneses indukciója tehát a hatszög középpontjában \(\displaystyle 2B_0=0{,}2~\rm mT\) nagyságú, iránya pedig a lefelé folyó áram által létrehozott indukcióval megegyező (vagyis a hatszög azonos irányú áramoknak megfelelő csúcspontjait összekötő húrral párhuzamos).
\(\displaystyle b)\) A felfelé folyó áramú vezetők 1 m hosszú darabjaira ható erő nagysága \(\displaystyle 5{,}8\cdot10^{-4}\) N, iránya az áramvezetőhöz tartozó csúcspontot \(\displaystyle O\)-val összekötő egyenesre merőleges. A lefelé folyó áramú vezető 1 m hosszú darabjára ható erő nagysága \(\displaystyle 1{,}0\cdot10^{-3}\) N, iránya az áramvezetőhöz tartozó csúcspontot \(\displaystyle O\)-val összekötő egyenessel párhuzamos. (A felfelé folyó áramok vezetói egyméshoz közeledni akarnak, a lefelé folyó áramú vezeték pedig a másik kettőtől távolodni igyekszik.)
Statisztika:
37 dolgozat érkezett. 4 pontot kapott: Bekes Nándor, Bukor Benedek, Jakus Balázs István, Juhász 326 Dániel, Kopitkó Tünde, Molnár Mátyás, Németh 777 Róbert, Sal Kristóf, Szick Dániel. 3 pontot kapott: Bartók Imre, Csire Roland, Csorba Benjámin, Hornák Bence, Iván Balázs, Kluèka Vivien, Kormányos Hanna Rebeka, Körmöczi Dávid, Mándoki László, Mány Bence, Németh Flóra Boróka, Sallai Krisztina, Stein Ármin, Szőke Dániel, Török Péter, Varga-Umbrich Eszter, Veres Tamás, Wiandt Péter, Zöllner András. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2015. decemberi fizika feladatai
