A P. 4823. feladat (2016. március)

P. 4823. Rögzített, \(\displaystyle \alpha\) hajlásszögű lejtőn két (homogén tömegeloszlású) gömb az ábrán látható módon helyezkedik el. Feltéve, hogy a legördülő gömbök középpontját összekötő egyenes végig függőleges marad, mekkora lehet az \(\displaystyle \alpha\) szög? Mekkora a testek gyorsulása ekkor?

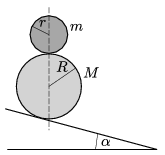
(A tapadó súrlódás elég nagy, és a közegellenállás elhanyagolható.)

Közli: Iván Balázs (Fonyód, Mátyás Király Gimnázium)

(5 pont)

A beküldési határidő 2016. április 11-én LEJÁRT.

Megoldás. Ha mindkét test tömegközéppontja \(\displaystyle a\) gyorsulással mozog a lejtő esésvonalának irányában, a felső gömb (golyó) szöggyorsulása (a csúszásmentes gördülés feltétele miatt) \(\displaystyle a/r\). Ha a felső golyóra az alsó \(\displaystyle F\) nagyságú, vízszintes irányú súrlódási erőt fejt ki, akkor a felső golyó vízszintes irányú mozgásának egyenlete:

\(\displaystyle F=ma\cos\alpha,\)

hiszen a felső testre ható többi erőnek (a nehézségi erőnek és az alsó golyó által kifejtett függőleges irányú tartóerőnek) nincs vízszintes komponense.

A felső, \(\displaystyle \tfrac25mr^2\) tehetetlenségi nyomatékú golyó forgómozgásának egyenlete:

\(\displaystyle Fr=\frac25mr^2\cdot \frac{a}{r},\)

mert a golyóra ható többi erőnek (a nehézségi erőnek és az alsó golyó által kifejtett függőleges irányú tartóerőnek) nincs forgatónyomatéka a gömb középpontjára vonatkoztatva.

A fenti 2 egyenlet hányadosából \(\displaystyle \cos\alpha=\tfrac25\), vagyis \(\displaystyle \alpha=66{,}4^\circ\) adódik, tehát csak ekkora hajlásszögű lejtőnél valósulhat meg a feladatban szereplő (meglehetősen ,,instabil'') mozgás.

A testek gyorsulásának nagyságát legegyszerűbben a munkatételből határozhatjuk meg. Egy bizonyos \(\displaystyle t\) idő alatt a két test tömegközéppontja \(\displaystyle at^2/2\) utat tesz meg, sebességük \(\displaystyle at\), szögsebességük pedig \(\displaystyle at/R\), illetve \(\displaystyle at/r\) lesz. A munkatétel szerint:

\(\displaystyle (M+m)g\cdot \frac{a}{2}t^2\, \sin\alpha=\frac{1}{2}M(at)^2+ \frac{1}{2}m(at)^2+\frac{1}{2}\cdot\frac25MR^2\cdot \left(\frac{a}{R}\,t\right)^2+ \frac{1}{2}\cdot\frac25mr^2\cdot \left(\frac{a}{r}\,t\right)^2, \)

ahonnan egyszerűsítések és a lejtő hajlásszögének már kiszámított értékének felhasználása után kapjuk:

\(\displaystyle a=\frac57\,g\sin\alpha=\sqrt{\frac{3}{7}}\,g\approx 6{,}4~\rm m/s^2.\)

A fenti eredmények természetesen a haladó- és a forgómozgás összesen 6 egyenletének felírása és megoldása után is megkaphatóak. (Az ismeretlenek: 4 kényszererő és a testek gyorsulása.) Az egyenletrendszer túlhatározott, ami azt mutatja, hogy a leírt mozgás csak bizonyos hajlásszögű lejtő esetén valósulhat meg.

Statisztika:

29 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Csorba Benjámin, Di Giovanni András, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Forrai Botond, Gergely 444 Kornél, Ghada Alshalan, Iván Balázs, Kasza Bence, Körmöczi Dávid, Marozsák Tóbiás , Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Sal Kristóf, Szentivánszki Soma , Tófalusi Ádám, Tomcsányi Gergely, Varga-Umbrich Eszter, Zöllner András.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2016. márciusi fizika feladatai