 |
A P. 4826. feladat (2016. március) |
P. 4826. Síkkondenzátor párhuzamos lemezeinek \(\displaystyle Q_1={2\cdot10^{-5}}\) C, illetve \(\displaystyle Q_2=5\cdot10^{-5}\) C töltést adtunk, majd a lemezek közé, azokkal párhuzamosan, a lemezek területével megegyező alapterületű töltetlen fémhasábot toltunk. Mekkora töltés található a fémhasáb bal és jobb oldali felületén?
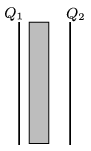
Közli: Kotek László, Pécs
(4 pont)
A beküldési határidő 2016. április 11-én LEJÁRT.
Megoldás. Ha mindkét lemezre ugyanakkora (és egyforma előjelű) \(\displaystyle Q\) töltést vittünk volna, azok elektromos erőtere szimmetrikusan, a lemezektől kifelé mutatna, a lemezek között (gyakorlatilag) nem hozna létre elektromos térerősséget. Ha viszont a lemezekre ellentétes előjelű, \(\displaystyle \pm q\) töltést juttatnánk (ez a szokásos síkkondenzátor esete), akkor ezek erőtere a lemezeken kívűl lenne elhanyagolhatóan kicsi, a lemezek között viszont (jó közelítéssel) homogén térerősség alakulna ki. Amennyiben a lemezek közé még egy semleges fémhasábot is helyezünk, annak belsejében nulla lesz az elektromos térerősség, oldallapjaira viszont \(\displaystyle \mp q\) töltés kerül (elektromos megosztás). Ha például a jobb oldali lemez töltése \(\displaystyle +q\), akkor a fémhasáb jobb oldalán \(\displaystyle -q\), a bal oldalán pedig \(\displaystyle +q\) töltés ,,jelenik meg''.
A feladatban szereplő eset a két elrendeződés szuperpozíciójaként kezelhető. Az egyes lemezekre kerülő töltések:
\(\displaystyle Q_2=Q+q, \qquad \text{illetve}\qquad Q_1=Q-q,\)
ahonnan
\(\displaystyle q=\frac{Q_2-Q_1}{2}=1{,}5\cdot10^{-5}~\rm C.\)
Ennyi töltés lesz a fémhasáb bal oldalán, a jobb oldalán pedig \(\displaystyle -q\).
Az eredmény független a fémhasáb vastagságától (természetesen az a lemezek távolságánál kisebb kell legyen), valamint a hasáb elhelyezkedésétől (a lemezektől mért távolságától).
Statisztika:
30 dolgozat érkezett. 4 pontot kapott: Babanics Gergely, Balogh Menyhért, Bartók Imre, Blum Balázs, Csire Roland, Csorba Benjámin, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Forrai Botond, Ghada Alshalan, Iván Balázs, Kasza Bence, Körmöczi Dávid, Mány Bence, Olosz Adél, Páhoki Tamás, Pécsi 117 Ildikó, Szentivánszki Soma , Szőke Dániel, Tófalusi Ádám, Varga-Umbrich Eszter. 3 pontot kapott: Osváth Botond, Sal Kristóf. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2016. márciusi fizika feladatai
