A P. 4854. feladat (2016. május)

P. 4854. Az ábrán látható ,,végtelen'' kapcsolásban minden ellenállás ugyanakkora \(\displaystyle R\) nagyságú, és mindegyik kondenzátor kapacitása ugyanakkora \(\displaystyle C\) értékű. Mekkora az eredő ellenállás, illetve az eredő kapacitás az \(\displaystyle A\) és \(\displaystyle B\) pontok között?

Közli: Zsigri Ferenc, Budapest

(5 pont)

A beküldési határidő 2016. június 10-én LEJÁRT.

Megoldás. Foglalkozzunk először az ellenállásokkal! Ha az \(\displaystyle A\) és \(\displaystyle B\) pontokra feszültséget kapcsolunk, akkor az \(\displaystyle A\) és \(\displaystyle B\) pontokat nem tartalmazó átló (a továbbiakban egyszerűen átló) összes csomópontja ekvipotenciális pont lesz, a közöttük lévő ellenállásokat tehát kiiktathatjuk a kapcsolásból (hiszen úgysem folyik át rajtuk áram). Az átló szimmetrikusan elhelyezkedő (ekvipotenciális) pontjait rövidre is zárhatjuk (úgysem fog áram folyni közöttük). Ilymódon a kapcsolás az alábbival egyenértékű:

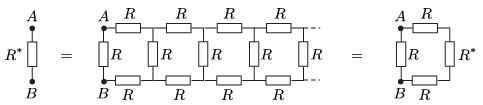
Így az \(\displaystyle R^*\) eredő ellenállásra a következő rekurziós összefüggést írhatjuk fel:

\(\displaystyle \frac{1}{R^*}=\frac{1}{R}+\frac{1}{2R+R^*},\)

amelynek (fizikailag értelmezhető, pozitív) megoldása:

\(\displaystyle {R^*}=(\sqrt{3}-1)R\approx 0{,}73\,R.\)

A kondenzátorokat tartalmazó kapcsolás eredője hasonló módon kapható meg, de közvetlenül is adódik az előző eredményből. Ha a hálózatot \(\displaystyle \omega\) körfrekvenciájú váltófeszültségre kapcsoljuk, a kondenzátorok \(\displaystyle R=\frac{1}{\omega C}\) nagyságú ,,ellenállásokkal'' helyettesíthetők. (A fázistolással nem kell foglalkoznunk, mert az mindegyik áramköri elemnél ugyanakkora, így az eredményt nem befolyásolja.) Ha az egész kapcsolás eredő kapacitása \(\displaystyle C^*\), akkor az \(\displaystyle R^*=\frac{1}{\omega C^*}\) ellenállással helyettesíthető. A korábbi eredmény felhasználásával

\(\displaystyle \frac{R^*}{R}=\sqrt{3}-1=\frac{C}{C^*},\)

ahonnan

\(\displaystyle C^*=\frac{C}{\sqrt{3}-1} \approx 1{,}37\,C.\)

Statisztika:

21 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Csorba Benjámin, Di Giovanni András, Fekete Balázs Attila, Ghada Alshalan, Jakus Péter János, Kasza Bence, Kovács Péter Tamás, Körmöczi Dávid, Nagy Nándor, Olosz Adél, Páhoki Tamás, Sal Kristóf, Szántó Benedek, Tófalusi Ádám, Tomcsányi Gergely, Zöllner András.
2 pontot kapott:	1 versenyző.

A KöMaL 2016. májusi fizika feladatai