 |
A P. 4865. feladat (2016. október) |
P. 4865. Két, egymásra merőleges, egyenes országúton egyenletes sebességgel halad két gépkocsi az ábra szerint. Kezdetben a járművek \(\displaystyle x_0=6\) km és \(\displaystyle y_0=3\) km távolságra voltak a kereszteződéstől. Az \(\displaystyle AO\) pályán haladó jármű sebessége \(\displaystyle v_1=36\) km/h. Mozgásuk során innen 9 perc alatt kerülnek egymáshoz legközelebbi helyzetbe.
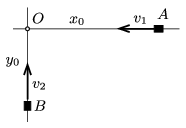
Mekkora a \(\displaystyle BO\) egyenesen haladó jármű sebessége, és mekkora a járművek között mérhető legkisebb távolság?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2016. november 10-én LEJÁRT.
Megoldás. I. (algebrai) megoldás. A két gépkocsi közötti távolság négyzete \(\displaystyle t\) idejű mozgás után:
\(\displaystyle d^2=(x_0-v_1t)^2+(y_0-v_2t)^2= \left(t\sqrt{v_1^2+v_2^2}-\frac{v_1x_0+v_2y_0}{\sqrt{v_1^2+v_2^2}}\right)^2+ x_0^2+y_0^2-\frac{(v_1x_0+v_2y_0)^2}{v_1^2+v_2^2}.\)
Ez a kifejezés akkor a legkisebb, amikor
\(\displaystyle t=\frac{ v_1x_0+v_2y_0 }{v_1^2+v_2^2}.\)
Ez \(\displaystyle v_2\)-re nézve egy másodfokú egyenlet, amelynek (pozitív) megoldása: \(\displaystyle v_2^{(1)}=25{,}6~\rm km/h\), és a hozzá tartozó minimális távolság: \(\displaystyle d_\text{min}^{(1)}=1{,}03~\rm km.\)
A fentebbi másodfokú egyenletnek van egy másik, a \(\displaystyle v_2<0\) tartományba eső megoldása is. Fizikailag ez annak felel meg, hogy a \(\displaystyle B\) pontban lévő jármű távolodik a kereszteződéstől: \(\displaystyle v_2^{(2)}=-5{,}62~{\rm km/h}\) és \(\displaystyle d_\text{min}^{(2)}=3{,}9~\rm km.\)
II. (geometriai) megoldás. Írjuk le a mozgást a \(\displaystyle B\) járműből (annak vonatkoztatási rendszeréből) nézve. Ebben a leírásban a \(\displaystyle B\) jármű áll, a másik pedig a \(\displaystyle (-v_1,v_2)\) vektorral jellemezhető (most még ismeretlen) irányban mozog (lásd az ábrát). (A vektor komponenseit az \(\displaystyle OA\), illetve az \(\displaystyle OB\) irányban tekintjük pozitívnak.)
Ha a két jármű \(\displaystyle t\) idő múlva kerül egymáshoz legközelebb, akkor ezen pillanatban az \(\displaystyle A\) pontból induló jármű távolsága az \(\displaystyle OB\) egyenestől \(\displaystyle x_0-v_1t\) lesz, vagyis a jármű a szaggatott vonallal jelölt egyenes valamelyik pontjába kerül.
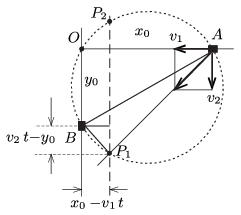
Másrészt a kérdéses pontban a két jármű közötti távolság minimális, tehát a relatív sebességük merőleges a járműveket összekötő egyenesre. Ezek szerint a kérdéses pont rajta fekszik az \(\displaystyle AB\) szakaszhoz tartozó Thalész-körön. Az ábrán látszik, hogy két ilyen pont is lehetséges, a \(\displaystyle v_2>0\)-hoz tartozó \(\displaystyle P_1\) pont, illetve a \(\displaystyle v_2<0\)-hoz tartozó \(\displaystyle P_2\) pont. A megfelelő derékszögű háromszögek hasonlóságát kihasználva felírhatjuk, hogy
\(\displaystyle \frac{v_1}{v_2}=\frac{v_2t-y_0}{x_0-v_1t},\)
ahonnan az ismert adatok behelyettesítése után a (km/h egységekben felírt) \(\displaystyle v_2\)-re ezt a másodfokú egyenletet kapjuk:
\(\displaystyle v_2^2-20v_2-144=0,\)
aminek a megoldásai: 25,6 és \(\displaystyle -5{,}6\), és ezek ismeretében a két jármű kérdezett távolsága is kiszámítható az egyes esetekben: \(\displaystyle BP_1=1{,}0~\rm km\), illetve \(\displaystyle BP_2=3{,}9~\rm km\)
Statisztika:
125 dolgozat érkezett. 5 pontot kapott: 66 versenyző. 4 pontot kapott: 6 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 18 versenyző. 1 pontot kapott: 22 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2016. októberi fizika feladatai
