A P. 4880. feladat (2016. november)

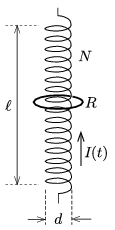
P. 4880. Egy \(\displaystyle d=4{,}4\) cm átmérőjű, \(\displaystyle \ell=1\) m hosszú, \(\displaystyle N=1000\) menetes egyenes tekercs közepén egy \(\displaystyle r=2{,}5\) cm sugarú, \(\displaystyle R=10^{-4}~\Omega\) ellenállású vastag körvezető gyűrű helyezkedik el koaxiálisan. A tekercsben folyó \(\displaystyle 50\) A erősségű áramot 1 s alatt \(\displaystyle -50\) A erősségűre változtatjuk.

\(\displaystyle a)\) Mekkora a mágneses indukció nagysága a körvezető középpontjában akkor, amikor a tekercs árama éppen nulla?

\(\displaystyle b)\) Mekkora ez az érték ezelőtt, illetve ezután \(\displaystyle \Delta t=0{,}001\) s idővel?

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2016. december 12-én LEJÁRT.

Megoldás. A tekercsben folyó, időben változó nagyságú áram által létrehozott mágneses fluxus:

\(\displaystyle \Phi(t)=\mu_0\frac{N I(t)}{\ell}\cdot \frac{d^2\pi}{4},\)

így a körvezető gyűrűben indukált feszültség nagysága

\(\displaystyle U=\frac{\Delta\Phi}{\Delta t}=\mu_0\frac{N d^2\pi}{4\ell}\cdot \frac{\Delta I(t)}{\Delta t}, \)

aminek hatására abban

\(\displaystyle I'=\frac{U}{R}=\mu_0\frac{N d^2\pi}{4\ell R}\cdot \frac{\Delta I(t)}{\Delta t}\)

áram indul meg. Az \(\displaystyle I(t)\) áram változási sebességének nagysága:

\(\displaystyle \left\vert\frac{\Delta I(t)}{\Delta t}\right\vert=100~\frac{\rm A}{\rm s}.\)

Mivel \(\displaystyle I(t)\) időben egyenletesen változik, \(\displaystyle U\) és \(\displaystyle I'\) is időben állandó, tehát a körvezetőnél önindukciós jelenséggel nem kell számolnunk.

\(\displaystyle a)\) Abban a pillanatban, amikor \(\displaystyle I(t)=0\), a tekercs saját mágneses tere is nulla, a körvezetőben folyó áram viszont a gyűrű középpontjában

\(\displaystyle B'=\mu_0\frac{I'}{2r}=\mu_0^2\frac{N d^2\pi}{8\ell rR}\cdot \frac{\Delta I(t)}{\Delta t}= \frac{(12{,}6\cdot10^{-7})^2\cdot 10^3\cdot 0{,}044^2\,\pi\cdot 10^2}{8\cdot 0{,}025\cdot 10^{-5}}~{\rm T}=0{,}05 ~{\rm mT} \)

nagyságú mágneses indukciót hoz létre.

\(\displaystyle b)\) A tekercsben folyó áram erőssége a kérdéses pillanatokban

\(\displaystyle I_1=\pm 100~\frac{\rm A}{\rm s}\cdot \Delta t=\pm 0{,}1~\rm A.\)

Ekkora áram a tekercs középpontjában

\(\displaystyle B= \mu_0\frac{N I_1}{\ell}=\pm 0{,}13~{\rm mT} \)

mágneses indukciót eredményez. (A tekercs által keltett mágneses indukció a tekercs tengelyével párhuzamos, iránya az áram irányától és a tekercselés irányától függ, de a két esetben biztosan ellentétes.)

Az eredő mágneses indukció a tekercs és a körvezető áramának együttes hatására jön létre. A tekercs időben csökkenő mágneses indukciója a körvezetőben olyan feszültséget indukál, amelynek hatására meginduló áram a változást mérsékeli (Lenz-törvény), tehát \(\displaystyle B'\) a tekercs \(\displaystyle B\) indukcióját növeli. Az eredő mágneses indukció nagysága ezek szerint az \(\displaystyle a)\) alkérdésben szereplő időpont előtt \(\displaystyle \Delta t\) idővel

\(\displaystyle \vert B_1\vert =\vert B(-\Delta t)+B'\vert =\vert 0{,}13~{\rm mT}+0{,}05~{\rm mT}\vert =0{,}18~{\rm mT}, \)

utána pedig

\(\displaystyle \vert B_2\vert =\vert B(+\Delta t)+B'\vert =\vert -0{,}13~{\rm mT}+0{,}05~{\rm mT}\vert =0{,}08~{\rm mT}. \)

Statisztika:

36 dolgozat érkezett.
5 pontot kapott:	Bekes Nándor, Faisal Fahad AlSallom, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Guba Zoltán, Iván Balázs, Kolontári Péter, Kovács 124 Marcell, Marozsák Tóbiás , Mocskonyi Mirkó, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Páhoki Tamás, Pécsi 117 Ildikó, Szentivánszki Soma , Tófalusi Ádám, Varga-Umbrich Eszter.
4 pontot kapott:	Di Giovanni András, Kondákor Márk, Magyar Róbert Attila, Pataki 245 Attila, Wesniczky Albert.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2016. novemberi fizika feladatai