A P. 4884. feladat (2016. december)

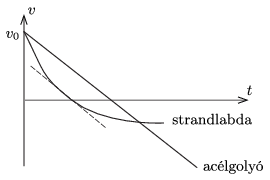
P. 4884. Néhány m/s sebességgel függőlegesen feldobunk egy pár cm átmérőjű acélgolyót, valamint ugyanakkora sebességgel egy könnyű, nagy strandlabdát. Ábrázoljuk vázlatosan a mozgás sebesség–idő grafikonját ugyanabban a koordináta-rendszerben!

Hasonlítsuk össze a testek kiindulási és visszaérkezési sebességét! Van-e olyan pillanat, amikor a két görbe meredeksége megegyezik? Melyik test jut magasabbra, és ez hogyan látszik a grafikonon?

Közli: Honyek Gyula, Budapest

(4 pont)

A beküldési határidő 2017. január 10-én LEJÁRT.

Megoldás. A golyó mozgásegyenlete (ha a felfelé mutató irányt választjuk pozitívnak és a közegellenállást elhanyagoljuk):

\(\displaystyle a_\textrm{golyó}= \frac{\Delta v_\textrm{golyó}}{\Delta t}=-g.\)

A golyó sebessége időben egyenletesen változik (csökken), tehát a \(\displaystyle v-t\) grafikon egy egyenes. Az emelkedési magasság a grafikon \(\displaystyle v>0\) szakaszának ,,görbe'' alatti területével egyezik meg.

Az ábráról leolvasható, hogy a golyó magasabbra emelkedik, mint a labda, hiszen a labda hamarabb ér el a pályájának legmagasabb pontjába, mint a golyó, és az emelkedés közben a sebessége mindvégig kisebb, mint a golyó pillanatnyi sebessége.

A strandlabdára ható erő a nehézségi erő és a közegellenállási erő eredője. Ez utóbbi nagysága \(\displaystyle v^2\)-tel arányos, iránya pedig \(\displaystyle v\)-vel ellentétes, így a labda mozgásegyenlete:

\(\displaystyle a_\textrm{labda}= \frac{\Delta v_\textrm{labda}}{\Delta t}=-g-k\cdot v_\textrm{labda} \vert v_\textrm{labda}\vert,\)

(ahol \(\displaystyle k\) egy állandó). Mindaddig, amíg \(\displaystyle v_\textrm{labda}>0\), a labda sebessége gyorsabb ütemben csökken, mint a golyóé, és a két görbe meredeksége éppen a labda visszafordulásának pillanatában egyezik meg.

A két test kezdősebessége megegyezik, így a kezdeti mechanikai energiájuk is egyforma. A leérkezés pillanatában a helyzeti energiák megegyeznek, de a labda összes mechanikai energiája kisebb, mint a golyóé, hiszen a közegellenállás munkája a mozgás közben mindvégig csökkentette a mechanikai energiát. Emiatt a labda sebességének nagysága a leérkezés pillanatában biztosan kisebb, mint a golyóé.

Statisztika:

33 dolgozat érkezett.
4 pontot kapott:	Di Giovanni András, Fehér 169 Szilveszter, Kozák András, Markó Gábor, Merkl Gergely, Morvai Orsolya, Nagy 555 Botond, Nyerges Dóra, Stefán Boglárka Abigél, Szalay Gergő, Turcsányi Ádám.
3 pontot kapott:	Csuha Boglárka, Faisal Fahad AlSallom, Háder Márk István, Hajdu 046 Ákos, Jánosdeák Márk, Klučka Vivien, Krasznai Anna, Makovsky Mihály, Mocskonyi Mirkó, Wolff Vilmos.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2016. decemberi fizika feladatai