A P. 4900. feladat (2017. január)

P. 4900. Érdekes optikai játék két egymással szembefordított, azonos görbületi sugarú, homorú gömbtükör, melyek közül a felső tükör közepén egy néhány centiméter átmérőjű, kör alakú lyuk van. A tükrök olyan távolságra vannak egymástól, hogy az alsó tükör közepére tett kicsiny tárgy (például egy szem cukor) képe a lyukas tükör közepén jelenik meg, miután a tárgyról induló fénynyaláb előbb a felső, azután az alsó tükörről is egyszer visszaverődött.

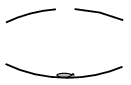
$\displaystyle a)$ Milyen messze lehet egymástól a két tükör közepe?

$\displaystyle b)$ Egyenes vagy fordított állású, valódi vagy látszólagos a megjelenő kép, és mekkora a nagyítás?

Közli: Radnai Gyula, Budapest

(5 pont)

A beküldési határidő 2017. február 10-én LEJÁRT.

Megoldás. $\displaystyle a)$ Jelöljük a tükrök fókusztávolságát $\displaystyle f$-fel, az optikai tengely mentén mért távolságukat pedig $\displaystyle d$-vel. A felső tükör a $\displaystyle t_1=d$ távol lévő tárgyról a leképezési törvény szerint

$\displaystyle k_1=\frac{df}{d-f}$

távolságban alkot (valódi vagy látszólagos) képet. Ez a kép az alsó tükörtől

$\displaystyle t_2=d-k_1=\frac{d(d-2f)}{d-f}$

távol lévő tárgynak tekinthető, amelynek a képe (az alsó tükör felett)

$\displaystyle k_2=\frac{t_2f}{t_2-f}=\frac{fd(d-2f)}{d^2-3fd+f^2}$

magasságban képződik. A megadott feltétel szerint $\displaystyle k_2=d$, tehát

$\displaystyle \frac{fd(d-2f)}{d^2-3fd+f^2}=d,$

vagyis

$\displaystyle d^2-4df+3f^2=0.$

Ennek a másodfokú egyenletnek 2 valós gyöke van:

$\displaystyle d_1=f=\frac12R \qquad \text{és} \qquad d_2=3f=\frac32R.$

$\displaystyle b)$ A nagyítás

$\displaystyle N=\frac{k_1}{t_1}\frac{k_2}{t_2}=\frac{f^2}{d^2-3fd+f^2}.$

Ha $\displaystyle d=d_1=f$, akkor a nagyítás $\displaystyle -1$, tehát a kép fordított állású, ha pedig $\displaystyle d=d_2=3f$, akkor a nagyítás $\displaystyle +1$, tehát a kép egyenes állású. Mindkét esetben a kép valódi, vagyis ernyővel felfogható, de – megfelelő irányból nézve – szabad szemmel is látható. A képalkotás néhány nevezetes sugármenet segítségével könnyen megszerkeszthető.

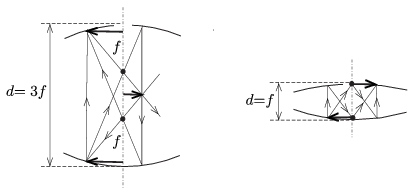
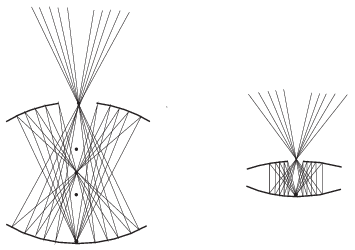
A szerkesztésnél használt segédvonalak nem mindegyike felel meg tényleges fénysugárnak, hiszen a felső tükör közepén egy lyuk van. Az alábbi ábrán a tárgy egy (az egyszerűség kedvéért az optikai tengelyen fekvő) pontjából kiinduló fénysugarakat ábrázoltuk a tükrök kétféle beállítása mellett. Látható, hogy az optikai tengely közelében van egy olyan tartomány, ahonnan nézve nem láthatjuk a lyuk közepén keletkező valódi képet (hanem csak az alsó tükör közepén lévő tárgyat). A furcsa, fent lebegni látszó képet csak kicsit ,,oldalról'' figyelhetjük meg.

Statisztika:

24 dolgozat érkezett.
5 pontot kapott:	Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Paulovics Péter, Szentivánszki Soma , Tóth 111 Máté .
4 pontot kapott:	Bekes Nándor, Molnár Mátyás, Varga-Umbrich Eszter.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2017. januári fizika feladatai