 |
A P. 5026. feladat (2018. április) |
P. 5026. Egy \(\displaystyle m\) tömegű és \(\displaystyle R\) sugarú, vékony gyűrűt kétféleképpen hozunk kis kitérésű lengésbe. Az egyik esetben egy \(\displaystyle r\) sugarú, vízszintes tengelyű hengerre fűzzük fel a gyűrűt, kissé kitérítjük, majd elengedjük. A másik esetben egy \(\displaystyle r\) hosszúságú, elhanyagolható tömegű, vékony tűt ragasztunk a gyűrűbe úgy, hogy a tű a gyűrű közepe felé mutasson, és a gyűrű erre a tűre támaszkodjon lengés közben. A gyűrű mindkét esetben síkmozgást végez.
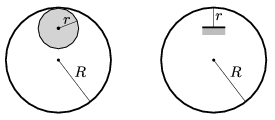
Melyik esetben hosszabb a lengésidő?
Közli: Radnai Gyula, Budapest
(5 pont)
A beküldési határidő 2018. május 10-én LEJÁRT.
Megoldás. A tű hegye körül elforduló gyűrű egy fizikai inga, amelynek lengésideje (kis kitérések esetén)
\(\displaystyle T_1=2\pi\sqrt{\frac{ mR^2+m(R-r)^2}{mg(R-r)}}=2\pi\sqrt{\frac{ 2R^2+r^2-2rR}{ g(R-r)}}.\)
A hengeren csúszásmentesen gördülő gyűrű mozgása bonyolultabb, hiszen a pillanatnyi forgástengely (a karika és a henger \(\displaystyle A\) érintkezési pontja) pillanatról pillanatra változó helyen található. Jelöljük a gyűrű \(\displaystyle A\) körüli szögsebességét \(\displaystyle \Omega_A\)-val! A gyűrű mozgási energiája ekkor
\(\displaystyle E_\text{mozgási}=\frac{1}{2}I_A\Omega_A^2,\)
ahol a Steiner-tétel szerint \(\displaystyle I_A=2mR^2\).
Fejezzük ki a mozgási energiát a henger (időben állandó helyzetű) \(\displaystyle P\) ,,középpontja'' körüli elfordulás \(\displaystyle \Omega_P\) szögsebessége segítségével! Mivel a gyűrű \(\displaystyle K\) középpontjának sebessége kétféle módon is felírható:
\(\displaystyle v_K=R\Omega_A=(R-r)\Omega_P,\)
tehát
\(\displaystyle \Omega_A=\frac{R-r}{R}\Omega_P,\)
és így a mozgási energia
\(\displaystyle E_\text{mozgási}=m(R-r)^2\Omega_P^2.\)
Ha az \(\displaystyle AK\) egyenes \(\displaystyle \varphi\) szöget zár be a függőlegessel, akkor a karika gravitációs helyzeti energiája
\(\displaystyle E_\text{helyzeti}=mg(R-r)(1-\cos\varphi)=mg(R-r)\cdot 2\sin^2\frac{\varphi}{2}\approx mg(R-r)\frac{\varphi^2}{2}.\)
Tudjuk továbbá, hogy
\(\displaystyle \Omega_P=\frac{\Delta\varphi}{\Delta t},\)
vagyis \(\displaystyle \Omega_P\) az időben változó \(\displaystyle \varphi(t)\) változási sebessége (deriváltja).
A harmonikus rezgőmozgás képleteit használva felírhatjuk:
\(\displaystyle \varphi(t)=\varphi_\text{max} \sin\omega t,\)
\(\displaystyle \Omega_P(t)=\varphi_\text{max} \omega \cos\omega t,\)
ahol \(\displaystyle \omega=2\pi/T\) (\(\displaystyle T\) a rezgés periódusideje).
Ezek ismeretében megadhatjuk a helyzeti és a mozgási energia időbeli változásának képleteit:
\(\displaystyle E_\text{helyzeti}(t)= \frac{1}{2}mg(R-r) \varphi_\text{max}^2\sin^2(\omega t), \)
\(\displaystyle E_\text{mozgási}(t)= m(R-r)^2\omega^2 \varphi_\text{max}^2\cos^2(\omega t). \)
A gyűrű teljes energiája időben állandó mennyiség:
\(\displaystyle E=E_\text{helyzeti}(t)+E_\text{mozgási}(t)=\text{állandó}+\frac{1}{2}mg(R-r) \varphi_\text{max}^2\cos^2(\omega t)\left[\frac{2\omega^2(R-r)}{g}-1\right]. \)
Ez az energia akkor nem függ az időtől, ha a szögletes zárójelben álló kifejezés nulla, vagyis
\(\displaystyle \omega=\sqrt{\frac{g}{2(R-r)}},\)
és így a ,,gördüléses rezgőmozgás'' periódusideje
\(\displaystyle T_2=2\pi\frac{2(R-r)}{g}.\)
Megmutatjuk, hogy \(\displaystyle T_1>T_2\), tehát a tű csúcsán billegő gyűrű lengésideje nagyobb, mint a gördülő gyűrűé. Valóban (a fizikailag megvalósítható \(\displaystyle 0<r<R\) tartományban)
\(\displaystyle \left(\frac{T_1}{T_2}\right)^2=\frac{2R^2+r^2-2Rr}{2(R-r)^2 } = 1+\frac{r(2R-r)}{2(R-r)^2}>1. \)
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Elek Péter, Marozsák Tóbiás , Olosz Adél, Sal Dávid. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2018. áprilisi fizika feladatai
