A P. 5083. feladat (2018. december)

P. 5083. Egy lejtő hajlásszöge \(\displaystyle \alpha\), rajta a súrlódási együttható \(\displaystyle \mu\). A lejtőn lévő \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű, kis méretű korongra mozgása közben hat egy \(\displaystyle B\) nagyságú, a lejtő síkjára merőleges irányú homogén mágneses tér is. A korongot kezdősebesség nélkül elengedjük. Határozzuk meg a korong állandósult sebességének nagyságát és irányát!

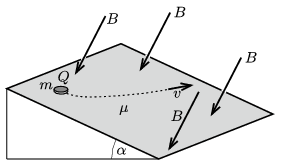
(A feladat ábrája a KöMaL nyomtatott számában fordított irányú mágneses mezővel jelent meg. Az ott vázolt mozgásirány a \(\displaystyle Q<0\) esetnek felel meg.)

A Kvant nyomán

(5 pont)

A beküldési határidő 2019. január 10-én LEJÁRT.

Megoldás. Jelöljük a korong állandósult sebességének nagyságát \(\displaystyle v\)-vel, irányának a lejtő szintvonalaival bezárt szögét \(\displaystyle \beta\)-val (lásd az ábrát, ami a lejtő síkjára merőleges irányú nézet). Az ábrán látható előjelek \(\displaystyle Q>0\) esetén érvényesek. \(\displaystyle Q<0\) (vagy fordított irányú mágneses mező) esetén a korong pályája ellenkező irányban (,,felénk'') térül el.

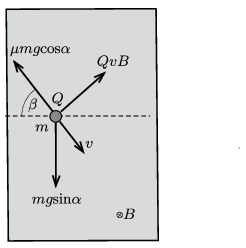
A mozgásegyenletek:

\(\displaystyle mg\sin\alpha\sin\beta=\mu mg\cos\alpha,\)

\(\displaystyle mg\sin\alpha\cos\beta=QvB. \)

A fenti egyenletek négyzetösszegéből

\(\displaystyle v=\frac{mg\cos\alpha}{QB}\sqrt{\tg^2\alpha-\mu^2},\)

az egyenletek arányából pedig

\(\displaystyle \tg\beta=\frac{\mu}{\sqrt{\tg^2\alpha-\mu^2}}\)

következik.

A fenti képletek csak \(\displaystyle \mu<\tg\alpha\) esetben érvényesek. Amennyiben \(\displaystyle \mu>\tg\alpha\), a korong nem jön mozgásba, illetve ha meglökjük, hamarosan megáll, tehát az állandósult sebessége nulla lesz.

Statisztika:

39 dolgozat érkezett.
5 pontot kapott:	Békési Ábel, Bokor Endre, Bonifert Balázs, Bukor Benedek, Csépányi István, Elek Péter, Fiam Regina, Hervay Bence, Keltai Dóra, Kozák 023 Áron, Mácsai Dániel, Markó Gábor, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Morvai Orsolya, Murányi Albert, Olosz Adél, Pácsonyi Péter, Sal Dávid, Somogyi Boglárka Zsófia, Szabó 314 László, Tiefenbeck Flórián, Varga Vázsony, Vaszary Tamás, Viczián Anna.
4 pontot kapott:	Andorfi István, Hisham Mohammed Almalki, Lipták Gergő, Makovsky Mihály, Szoboszlai Szilveszter, Tafferner Zoltán, Tran Quoc Dat, Vajay Mónika, Vass Bence.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2018. decemberi fizika feladatai