 |
A P. 5088. feladat (2018. december) |
P. 5088. Egy \(\displaystyle \ell\) hosszúságú fonálingát vízszintesen kitérítünk, majd elengedünk. Amikor a fonál eléri a függőleges helyzetét, egy szögbe ütközik, s innen kezdve már csak az alsó, \(\displaystyle r\) hosszúságú része lendül tovább.
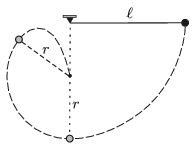
Mekkora az \(\displaystyle r/\ell\) arány, ha az ingatest, miután felfelé haladva letér valahol a körpályáról, szabadon mozogva pontosan a szögbe ütközik?
Közli: Radnai Gyula, Budapest
(6 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
Megoldás. Amikor az ingatest már a szög ,,túlsó oldalán'' felfelé halad és az inga fonala \(\displaystyle \alpha\) szöget zár be a függőlegessel (lásd az ábrát), az energiamegmaradás törvénye szerint a sebessége:
| \(\displaystyle (1)\) | \(\displaystyle v=\sqrt{2g(\ell-r-r\cos\alpha)},\) |
a fonalát feszítő erő pedig (a Newton-egyenlet alapján):
\(\displaystyle N=\frac{mv^2}{r}-mg\cos\alpha.\)
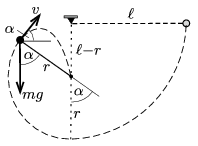
Ha \(\displaystyle N\) nullává válik, majd negatív lesz, a fonál meglazul. Határesetben (amikor a meglazulás elkezdődik):
| \(\displaystyle (2)\) | \(\displaystyle v^2=gr\cos\alpha,\) |
vagyis (1) felhasználásával
| \(\displaystyle (3)\) | \(\displaystyle \frac{\ell}{r}=\frac{3}{2}\cos\alpha+1.\) |
A \(\displaystyle v\) kezdősebességgel \(\displaystyle \alpha\) szögben elinduló, majd szabadon eső ingatest akkor ütközik \(\displaystyle t\) idő múlva a szögnek, ha fennáll, hogy
| \(\displaystyle (4)\) | \(\displaystyle vt\cos\alpha=r\sin\alpha,\) |
| \(\displaystyle (5)\) | \(\displaystyle vt\sin\alpha-\frac{g}{2}t^2=-r\cos\alpha.\) |
(4)-ből az időt kifejezve és (5)-be helyettesítve
\(\displaystyle \frac{2v^2}{rg\cos\alpha}=\tg^2\alpha\)
adódik, amiből (2) felhasználásával
\(\displaystyle \tg\alpha=\sqrt{2}, \qquad \text{vagyis} \qquad \alpha\approx 54{,}7^\circ\)
következik. A keresett hosszúságarány (3) szerint
\(\displaystyle \frac{r}{\ell}=2\left(2-\sqrt3\right)\approx 0{,}54.\)
Statisztika:
39 dolgozat érkezett. 6 pontot kapott: Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Bukor Benedek, Csépányi István, Elek Péter, Fekete András Albert, Fiam Regina, Fülöp Sámuel Sihombing, Hisham Mohammed Almalki, Horváth 999 Anikó, Kovács 111 Bence, Lipták Gergő, Mácsai Dániel, Makovsky Mihály, Markó Gábor, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Rusvai Miklós, Sal Dávid, Tiefenbeck Flórián, Tran Quoc Dat, Varga Vázsony, Vaszary Tamás, Virág Levente. 5 pontot kapott: Hervay Bence, Merkl Gergely, Viczián Anna. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2018. decemberi fizika feladatai
