 |
A P. 5099. feladat (2019. január) |
P. 5099. Egy hullámvasút kocsija egy függőleges síkban fekvő, kör alakú pályán halad úgy, hogy a saját motorját és fékjét használva a sebességét állandó értéken tartja. Legalább mekkora sebességet kell tartania ahhoz, hogy az \(\displaystyle R\) sugarú pályán megcsúszás nélkül tudjon végighaladni, ha a tapadó súrlódás együtthatója \(\displaystyle \mu\)? Hol csúszna meg, ha a sebessége ennél kicsit kisebb lenne? A kocsi elég kicsi a pálya sugarához képest.
Közli: Takács László, Baltimore, USA
(6 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldás. Jelöljük az \(\displaystyle m\) tömegű kocsi (állandó) sebességét \(\displaystyle v_0\)-lal, a sínek által kifejtett, sugárirányú nyomóerőt \(\displaystyle N\)-nel, az érintő irányú súrlódási erőt \(\displaystyle S\)-sel, és a kocsi pillanatnyi helyzetét adjuk meg az 1. ábrán látható \(\displaystyle \varphi\) szöggel. Legyen a kocsi tömege \(\displaystyle m\), a rá ható nehézségi erő tehát \(\displaystyle mg\).
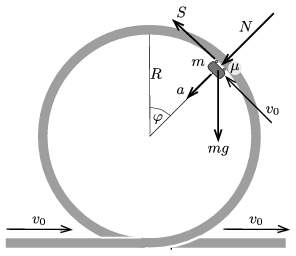
1. ábra
A kocsi egyenletes körmozgást végez, a gyorsulása tehát a pálya középpontja felé mutató,
\(\displaystyle a=\frac{v_0^2}{R}\)
nagyságú vektor. A Newton-féle mozgásegyenletek:
\(\displaystyle mg\sin\varphi-S=0,\)
\(\displaystyle mg\cos\varphi+N=m\frac{v_0^2}{R},\)
ahonnan
| \(\displaystyle (1)\) | \(\displaystyle S=mg\sin\varphi,\) |
| \(\displaystyle (2)\) | \(\displaystyle N=m\frac{v_0^2}{R}-mg\cos\varphi.\) |
A kocsi akkor nem csúszik meg a sínen, ha a pálya minden pontjában (vagyis minden \(\displaystyle \varphi\) szögnél) teljesül, hogy
| \(\displaystyle (3)\) | \(\displaystyle \mu>\frac{\vert S\vert}{N}\equiv \frac{\vert\sin\varphi\vert}{k-\cos\varphi},\) |
ahol
\(\displaystyle k=\frac{v_0^2}{Rg}\)
a sebesség nagyságára jellemző dimenziótlan szám. Az \(\displaystyle N\) nyomóerő legkisebb értékét a pálya legmagasabb pontjában, \(\displaystyle \varphi=0\)-nál éri el. Nyilván még itt is teljesülnie kell az \(\displaystyle N>0\) feltételnek (ellenkező esetben a kocsi elválik a sínektől), vagyis (2) alapján
\(\displaystyle m\frac{v_0^2}{R}>mg, \qquad \text{azaz}\qquad k>1.\)
Ahhoz, hogy a kocsi semelyik \(\displaystyle \varphi\) szögnél ne csússzon meg, a tapadó súrlódási együttható nagyobb kell, hogy legyen
| \(\displaystyle (4)\) | \(\displaystyle f(\varphi)\equiv \frac{\sin\varphi}{k-\cos\varphi} \) |
legnagyobb értékénél. Ha (3) éppen nem teljesülne (vagyis \(\displaystyle v_0\) egy ,,kicsit kisebb'' lenne a kritikus értéknél, akkor a kocsi az \(\displaystyle f(\varphi)\) függvény maximumához tartozó \(\displaystyle \varphi_0\) szög közelében megcsúszna. Feladatunk tehát a továbbiakban a (4)-ben megadott \(\displaystyle f(\varphi)\) függvény maximumhelyének és a maximum nagyságának meghatározása.
Megjegyzés. Elegendő a \(\displaystyle 0\le\varphi\le 180^\circ\) tartományban vizsgálódnunk, ekkor a kocsi ,felfelé'' halad. A ,,lefelé'' mozgó kocsinál, amikor \(\displaystyle -180^\circ\le\varphi\le 0\), a csúszásmentes mozgás feltétele ugyanaz, mint a felfelé haladó kocsinál, hiszen \(\displaystyle S(-\varphi)=-S(\varphi)\) és \(\displaystyle N(-\varphi)=N(\varphi)\).)
Ennek a (matematikai) problémának többféle módon is nekikezdhetünk:
I. (geometriai) módszer. Tekintsünk egy egységnyi hosszúságú pálcát, amelyet egy vízszintes egyenesre fektettünk. + A pálcát az egyik \(\displaystyle (P)\) végpontja körül \(\displaystyle \varphi\) szöggel elforgatjuk (2. ábra).
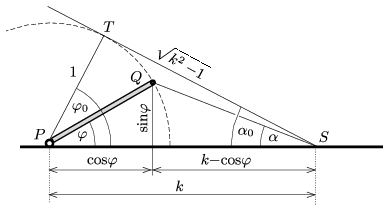
2. ábra
Ha a vízszintes egyenesre illeszkedő, a forgásponttól \(\displaystyle k\) távolságban található \(\displaystyle S\) pontból szemléljük a pálca másik \(\displaystyle (Q)\) végpontját, azt a vízszinteshez képest
\(\displaystyle \alpha=\arctg\frac{\sin\varphi}{k-\cos\varphi}\equiv \arctg f(\varphi)\)
szögben látjuk. Az \(\displaystyle \alpha\) hegyesszög legnagyobb értéke \(\displaystyle f(\varphi)\) maximális értékét is megadja:
\(\displaystyle (\tg\alpha)_\text{max}=f_\text{max},\)
és a maximum helyét is meghatározza:
\(\displaystyle f\left(\varphi_0\right)= f_\text{max}.\)
Mivel a pálca forgatása közben a \(\displaystyle Q\) pont egy körív mentén mozog, \(\displaystyle \alpha\) legnagyobb értékét akkor kapjuk, amikor \(\displaystyle ST\) érinti ezt a kört, vagyis a \(\displaystyle PTS\) háromszög derékszögű. Innen következik, hogy
| \(\displaystyle (5)\) | \(\displaystyle \cos\varphi_0=\frac{1}{k},\) |
továbbá
\(\displaystyle f_\text{max}=\tg\alpha_0=\frac{1}{\sqrt{k^2-1}}.\)
A hullámvasút kocsija tehát akkor tud csúszásmentesen végighaladni a függőleges síkú körpályán, ha
| \(\displaystyle (6)\) | \(\displaystyle \mu>\frac{1}{\sqrt{k^2-1}},\) |
illetve ennek megfordítása,
\(\displaystyle k=\frac{v_0^2}{Rg}>\sqrt{\frac{1}{\mu^2}+1}\)
teljesül.
II. (trigonometriai) módszer. A meg nem csúszás (3) feltétele az \(\displaystyle \varepsilon\) súrlódási határszög (\(\displaystyle \mu=\tg\varepsilon\)) bevezetésével így írható fel:
\(\displaystyle \frac{\sin\varepsilon}{\cos\varepsilon}>\frac{\sin\varphi}{k-\cos\varphi},\)
vagyis
\(\displaystyle k\sin\varepsilon >\sin\varphi\cos\varepsilon+\cos\varphi\sin\varepsilon, \)
azaz
| \(\displaystyle (7)\) | \(\displaystyle k\sin\varepsilon>\sin(\varphi+\varepsilon).\) |
Ez az egyenlőtlenség biztosan teljesül, ha
| \(\displaystyle (8)\) | \(\displaystyle \sin\varepsilon>\frac{1}{k},\) |
azaz
\(\displaystyle \mu=\tg\varepsilon=\frac{1}{\sqrt{\frac{1}{\sin^2\varepsilon}-1}}>\frac{1}{\sqrt{k^2-1}}. \)
Ez éppen a (6) egyenlőtlenség.
Amennyiben (6) éppen nem teljesül (vagyis \(\displaystyle \sin\varepsilon\approx (1/k)\)), akkor \(\displaystyle \varphi=\varphi_0\approx 90^\circ-\varepsilon\) szögnél a kocsi megcsúszik, hiszen itt válik a (7) egyenlőtlenség élessé. A megcsúszás helyét így is megadhatjuk:
\(\displaystyle \cos\varphi_0=\sin\varepsilon\approx \frac{1}{k},\)
összhangban a geometriai módszerrel kapott (5) összefüggéssel.
III. (differenciálszámításos) módszer. A (4) képlettel megadott függvény szélsőértékét (maximumát) a deriváltjának eltűnéséből is meg lehet kapni:
\(\displaystyle f'(\varphi)=\frac{(k-\cos\varphi)\cos\varphi-\sin^2\varphi}{(k-\cos\varphi)^2} \equiv \frac{k\cos\varphi-1}{(k-\cos\varphi)^2}=0.\)
Ez akkor teljesül, ha
\(\displaystyle \varphi=\varphi_0\qquad \text{ahol}\qquad \cos\varphi_0=\frac{1}{k},\)
továbbá
\(\displaystyle f_\text{max}=f(x_0)=\frac{1}{\sqrt{k^2-1}},\)
ahogy azt már korábban is megkaptuk.
Érdemes megvizsgálni két szélsőséges esetet. Ha \(\displaystyle \mu\gg 1\), vagyis a tapadó súrlódás igen nagy (ezt pl. a fogaskerekes megoldás valósítja meg legjobban), akkor a kritikus helyzetben (a megcsúszás határhelyzetében) \(\displaystyle v_0\approx \sqrt{Rg}\) és \(\displaystyle \varphi_0\approx 0\). A vonat tehát olyan lassan mozoghat, hogy a pálya tetőpontjánál majdnem leesik, és a megcsúszás is itt, a tetőpont közelében következik be, ha a sebesség egy kicsivel alacsonyabb a szükségesnél.
Ha viszont \(\displaystyle \mu\ll 1\) (a pálya nagyon csúszós), akkor \(\displaystyle v_0\gg \sqrt{Rg}\) (tehát a vonatnak igen gyorsan kell haladnia), és ha mégis megcsúszik, az \(\displaystyle \varphi_0\approx 90^\circ\)-nál, vagyis a pálya függőleges szakaszánál fog bekövetkezni.
Statisztika:
24 dolgozat érkezett. 6 pontot kapott: Andorfi István, Bokor Endre, Csépányi István, Hisham Mohammed Almalki, Mácsai Dániel, Markó Gábor, Máth Benedek, Olosz Adél, Sal Dávid, Szabó 314 László, Tiefenbeck Flórián, Varga Vázsony. 5 pontot kapott: Hervay Bence, Marozsák Tádé. 4 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 4 versenyző.
A KöMaL 2019. januári fizika feladatai
