 |
A P. 5106. feladat (2019. február) |
P. 5106. Egyenlő oldalú háromszög keresztmetszetű, \(\displaystyle n_1=1{,}8\) abszolút törésmutatójú prizmára vékony fénysugarat bocsátunk úgy, hogy a fénysugár pályája a felezősíkra szimmetrikus legyen.
\(\displaystyle a)\) Mekkora a belépő fénysugár beesési szöge?
\(\displaystyle b)\) Mekkora a belépő sugár és a kilépő sugár közötti szög, az ún. deviáció?
\(\displaystyle c)\) Ezután az egymáshoz képest rögzített prizma-fényforrás rendszert egy \(\displaystyle {n_2=1{,}5}\) törésmutatójú folyadékba merítjük. Mekkora lesz ebben az esetben a deviáció?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2019. március 11-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A szimmetrikus pályán haladó fénysugár első törési szöge \(\displaystyle 30^\circ\), így a beesési szögre
\(\displaystyle \sin\alpha=n_1\sin 30^\circ=0{,}9;\qquad \alpha=64{,}16^\circ.\)
\(\displaystyle b)\) A fénysugár eltérülése mindkét törésnél az óramutató járásának irányában: \(\displaystyle \alpha-30^\circ\), a teljes deviáció tehát
\(\displaystyle \Delta_1=2(\alpha-30^\circ)=68{,}32^\circ.\)
\(\displaystyle c)\) A prizmának a folyadékra vonatkoztatott (relatív) törésmutatója: \(\displaystyle n=n_1/n_2=1{,}2.\) Az első határfelületnél a beesési szög a korábban kiszámított \(\displaystyle \alpha=68{,}32^\circ\). A törési szög \(\displaystyle \beta=\arcsin\left(\sin\alpha/n\right)=48{,}59^\circ\).
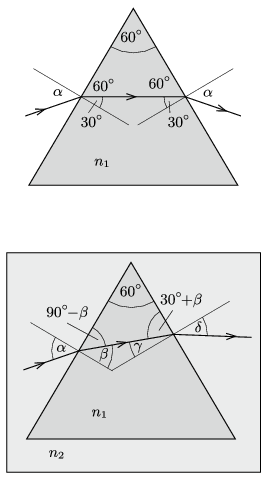
A második határfelületnél a beesési szög: \(\displaystyle \gamma= 60^\circ-\beta=11{,}41^\circ\), a törési szög pedig
\(\displaystyle \delta=\arcsin\left(n\cdot \sin\gamma\right)=13{,}73^\circ.\)
A deviáció a folyadékba merített prizma esetében:
\(\displaystyle \Delta_2=(\alpha-\beta)+(\delta-\gamma)=17{,}89^\circ,\)
ami \(\displaystyle \Delta_1-\Delta_2=50{,}43^\circ\)-kal kisebb eltérülést jelent, mint a levegőben levő prizmánál.
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Bekes Barnabás, Békési Ábel, Duong Phan, Fiam Regina, Fülöp Sámuel Sihombing, Hartmann Alice, Jánosik Áron, Keltai Dóra, Kertész Balázs, Lipták Gergő, Makovsky Mihály, Marozsák Tádé, Máth Benedek, Molnár Mátyás, Olosz Adél, Osvárt Bence Attila, Pácsonyi Péter, Rusvai Miklós, Sal Dávid, Schneider Anna, Schrott Márton, Sugár Soma, Tafferner Zoltán, Tiefenbeck Flórián, Vass Bence, Vaszary Tamás. 4 pontot kapott: Bonifert Balázs, Debreczeni Tibor, Merkl Gergely, Merkl Levente, Solymosi Réka. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2019. februári fizika feladatai
