A P. 5114. feladat (2019. március)

P. 5114. Egy asztal peremére illeszkedik egy \(\displaystyle \alpha\) hajlásszögű lejtő, amelyről egy \(\displaystyle \ell\) hosszúságú, \(\displaystyle d\) magasságú, homogén anyageloszlású, téglatest alakú hasáb csúszik le. Mennyivel nyúlik túl a hasáb az asztal peremén, amikor elkezd lebillenni, ha

\(\displaystyle a)\) a hasáb és a lejtő közötti súrlódás elhanyagolható;

\(\displaystyle b)\) a hasáb és a lejtő közötti súrlódási együttható \(\displaystyle \mu\)? (\(\displaystyle 0<\mu<\tg\alpha\), és \(\displaystyle \mu d<\ell\).)

Közli: Honyek Gyula, Veresegyház

(5 pont)

A beküldési határidő 2019. április 10-én LEJÁRT.

I. megoldás. A testre ható erők: \(\displaystyle mg\) nehézségi erő, a lejtő \(\displaystyle N\) nyomóereje, ami határesetben a lejtő alsó élénél, az \(\displaystyle O\) pontnál hat, valamint az \(\displaystyle S\) súrlódási erő (1. ábra). A hasáb a lejtőre merőlegesen nem gyorsul, így

\(\displaystyle N=mg\cos\alpha.\)

A súrlódási erő (mivel a hasáb csúszik):

\(\displaystyle S=\mu N=\mu mg \cos\alpha.\)

A test gyorsulása (a lejtő irányú eredő erőből számolva):

\(\displaystyle a=\frac{mg\sin\alpha-S}{m}=g(\sin\alpha-\mu \cos\alpha).\)

(A \(\displaystyle \mu\)-re megadott egyenlőtlenség miatt \(\displaystyle a>0\).)

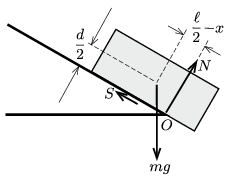
1. ábra

A hasáb mindaddig nem billen meg, amíg a rá ható erők forgatónyomatéka a tömegközéppontjára vonatkoztatva nulla. Határesetben (amikor az \(\displaystyle N\) erő erőkarja a lehető legnagyobb):

\(\displaystyle S\frac{d}{2}-N\left(\frac{\ell}{2}-x\right)=0,\)

vagyis

\(\displaystyle \frac{d}{2}\, mg\mu \cos\alpha=\left(\frac{\ell}{2}-x\right)\,mg\cos\alpha.\)

Innen a hasáb legnagyobb túlnyúlása az asztal peremén (a lejtő esésvonala mentén mérve):

\(\displaystyle x=\frac{\ell-\mu d}{2}.\)

Érdekes, hogy ez az eredmény nem függ a lejtő hajlásszögétől.

Amennyiben a súrlódás elhanyagolható, vagyis \(\displaystyle \mu=0\), a legnagyobb túlnyúlás: \(\displaystyle x=\frac{\ell}{2}\).

Megjegyzés. Ha a külső erők forgatónyomatékát nem a tömegközéppontra, hanem – mondjuk – a hasáb és a lejtő legalsó érintkezési pontjára írjuk fel, és ennek az eredő forgatónyomatéknak az eltűnését követeljük meg, hibás eredményt kapunk! Egyensúlyi állapotban a nyugvó testre ható erők forgatónyomatéka bármely pontra vonatkoztatva nulla, de a gyorsulva mozgó merev testekre ez általában már nem igaz. Helyes eredményt csak a tömegközéppontra és még néhány speciális helyzetű pontra felírt forgatónyomaték-egyensúlyi egyenletekből kapunk. Elterjedt tévhit, hogy a pillanatnyi forgástengely pontjai is ilyen speciális pontok, ez azonban általában nem igaz.

II. megoldás. A forgási egyensúly problémáját visszavezethetjük egy statikai feladatra, ha ,,beleülünk'' a téglatesttel együtt gyorsuló mozgást végző vonatkoztatási rendszerbe. Innen nézve a test (minden szempontból) egyensúlyban van, tehát a rá ható erők eredő forgatónyomatéka bármely pontra, így a lejtő és a lejtő alsó élénél lévő \(\displaystyle O\) pontra nézve is nulla. Nem szabad megfeledkeznünk arról, hogy ebben a gyorsuló koordináta-rendszerben fellép egy – a test tömegközéppontjában ható – \(\displaystyle ma\) nagyságú, a gyorsulással ellentétes irányú ún. tehetetlenségi erő is (2. ábra).

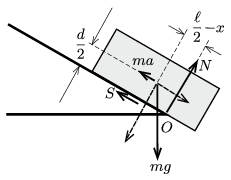
2. ábra

Az \(\displaystyle O\) pontra az \(\displaystyle N\) és az \(\displaystyle S\) erőnek nincs forgatónyomatéka, hanem csak a nehézségi erőnek és a tehetetlenségi erőnek. Ezek lejtő irányú komponense

\(\displaystyle mg\sin\alpha-ma=mg\sin\alpha-mg(\sin\alpha-\mu \cos\alpha)=\mu mg \cos\alpha,\)

\(\displaystyle d/2\) nagyságú erőkarral, a lejtőre merőleges erőkomponens pedig \(\displaystyle mg\cos\alpha\), az erőkar pedig \(\displaystyle (\ell/2-x).\) A forgatónyomatékok egyensúlyi egyenlete:

\(\displaystyle \frac{d}{2}\,\mu mg \cos\alpha=\left(\frac{\ell}{2}-x\right)\,mg\cos\alpha,\)

ahonnan

\(\displaystyle x=\frac{\ell-\mu d}{2}.\)

Statisztika:

31 dolgozat érkezett.
5 pontot kapott:	Bekes Barnabás, Békési Ábel, Bokor Endre, Bonifert Balázs, Elek Péter, Fekete Levente, Havasi Márton, Horváth 999 Anikó, Jánosik Áron, Kertész Balázs, Markó Gábor, Máth Benedek, Molnár Mátyás, Sal Dávid, Sas 202 Mór, Schneider Anna, Selmi Bálint, Szabó 314 László, Tiefenbeck Flórián, Toronyi András, Vass Bence.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2019. márciusi fizika feladatai