 Problem P. 5123. (April 2019)
Problem P. 5123. (April 2019)
P. 5123. There is a small object of mass \(\displaystyle m=0{.}25~\)kg at the left end of a trolley of mass \(\displaystyle M=1~\)kg and of length \(\displaystyle L=0.3~\)m. The trolley has vertical walls at its sides, and moves frictionlessly along the horizontal plane. Its small wheels are of negligible mass and size.
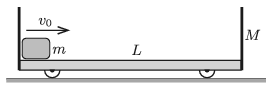
At a given instant the small object of mass \(\displaystyle m\) is given an initial speed of \(\displaystyle v_0=1~\)m/s towards the right. The coefficient of friction between the trolley and the object is \(\displaystyle \mu=0.1\). The collision between the object and the trolley can be considered elastic.
\(\displaystyle a)\) What is the speed of the trolley, when the object of mass \(\displaystyle m\) on it does not move with respect to the trolley?
\(\displaystyle b)\) How far is the object of mass \(\displaystyle m\) from the left wall of the trolley in the above asked case?
\(\displaystyle c)\) What are the velocities of the objects right after the moment of the first collision?
(5 pont)
Deadline expired on May 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A test és a kocsi között (ha azok sebessége különböző) \(\displaystyle \mu mg\) nagyságú súrlódási erő hat. \(\displaystyle \mu g\approx 1{,}0~\rm m/s^2\); a továbbiakban ezzel a közelítő értékkel fogunk számolni. \(\displaystyle m\) számszerű értékére nincs szükség, a megoldáshoz csak azt használjuk ki, hogy \(\displaystyle M=4m\).
\(\displaystyle a)\) A kocsi+test rendszerre nem hat vízszintes irányú külső erő, ezért a vízszintes irányú összes lendület állandó marad. Ha a kiskocsi és a hozzá képest nem mozgó test sebessége \(\displaystyle u\), akkor fennáll
\(\displaystyle mv_0=mu+Mu,\qquad \text{azaz}\qquad u=\frac{m}{m+M}v_0=\frac{1}{5}v_0=0{,}2~\frac{\rm m}{\rm s}.\)
\(\displaystyle b)\) Írjuk fel a munkatételt a kezdeti és a végállapot között! A súrlódási erő munkáját a kiskocsi és a test \(\displaystyle x\) nagyságú relatív elmozdulása határozza meg (1. ábra):
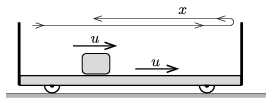
1. ábra
\(\displaystyle \frac{1}{2}(M+m)u^2-\frac{1}{2}mv_0^2=-\mu mgx,\)
ahonnan
\(\displaystyle x=\frac{2}{5}\,\frac{v_0^2}{\mu g}=0{,}4~{\rm m}=2L-0{,}2~{\rm m.}\)
Az \(\displaystyle m\) tömegű test tehát a kocsi bal oldali szélétől 20 cm távolságban lesz, amikor a relatív sebességük nullára csökken.
\(\displaystyle c)\) Legyen a kis test sebessége \(\displaystyle v_1\), a kocsi sebessége pedig \(\displaystyle v_2\) akkor, amikor a kis test eléri a kocsi jobb oldali szélét! (A sebességek irányát \(\displaystyle v_0\)-lal megegyező irányban tekintjük pozitívnak (2. ábra).)
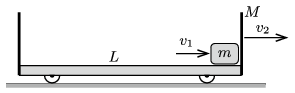
2. ábra
A lendületmegmaradás törvénye szerint
\(\displaystyle mv_0=mv_1+(4m)v_2,\)
a munkatétel pedig így alkalmazható:
\(\displaystyle \frac{1}{2}mv_1^2+\frac{1}{2}(4m)v_2^2-\frac{1}{2}mv_0^2=-\mu mgL.\)
(Ismét kihasználtuk, hogy a súrlódási erők munkájánál csak a két test relatív elmozdulását kell figyelembe vennünk.) A fenti egyenletek (ha az SI-mértékegységeket nem írjuk ki) igy alakulnak:
\(\displaystyle 1=v_1+4v_2,\)
\(\displaystyle 1=v_1^2+4v_2^2+0{,}6.\)
Ennek az egyenletrendszernek az egyik megoldása:
\(\displaystyle v_1=0{,}6~\frac{\rm m}{\rm s} \qquad \text{és}\qquad v_2=0{,}1~\frac{\rm m}{\rm s},\)
ami \(\displaystyle v_1>v_2\) miatt az ütközés előtti viszonyokat írja le. A másik megoldás:
\(\displaystyle v_1=-0{,}2~\frac{\rm m}{\rm s} \qquad \text{és}\qquad v_2=0{,}3~\frac{\rm m}{\rm s},\)
ami \(\displaystyle v_1<v_2\) miatt az ütközés utáni sebességeket adja meg.
Statistics:
37 students sent a solution. 5 points: Békési Ábel, Bokor Endre, Elek Péter, Fonyi Máté Sándor, Jánosik Áron, Keltai Dóra, Kertész Balázs, Mácsai Dániel, Makovsky Mihály, Markó Gábor, Marozsák Tádé, Merkl Gergely, Molnár Mátyás, Olosz Adél, Pácsonyi Péter, Sal Dávid, Tiefenbeck Flórián, Toronyi András, Varga Vázsony, Vass Bence, Vaszary Tamás, Viczián Anna. 4 points: Schneider Anna. 3 points: 5 students. 2 points: 3 students. 1 point: 6 students.
Problems in Physics of KöMaL, April 2019
