A P. 5165. feladat (2019. november)

P. 5165. Egységsugarú, homogén, kör alakú lemezből az ábrán látható módon kivágunk egymást kívülről érintő, rendre $\displaystyle \frac14, \frac18, \frac1{16}, \ldots$ sugarú, középpontjukkal az egyik sugárra illeszkedő köröket. Hol lesz a maradék idom tömegközéppontja, ha

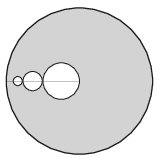
$\displaystyle a)$ csak a legnagyobb kört vágjuk ki;

$\displaystyle b)$ a két legnagyobb kört vágjuk ki;

$\displaystyle c)$ nagyon sok kört vágunk ki?

Közli: Tupi Zoltán, Budapest

(5 pont)

A beküldési határidő 2019. december 10-én LEJÁRT.

Megoldás. Jelöljük a $\displaystyle k$-adik kivágott kör sugarát $\displaystyle r_k$-val, tömegét $\displaystyle m_k$-val, a középpontjának távolságát az eredeti (tömör) körlemez középpontjától pedig $\displaystyle x_k$-val. Legyen továbbá a maradék lemez tömege $\displaystyle k$ darab kis kör kivágása után $\displaystyle M_k$. A távolságokat olyan egységekben számoljuk, amelyben az eredeti kör sugara 1, és a tömegeket is olyan módon adjuk meg, hogy az eredeti körlemez tömegének nagysága éppen 1 legyen.

A feladat szövege szerint

$\displaystyle r_1=\frac14,\quad r_2=\frac18,\quad \ldots \quad r_k=\frac1{2^{k+1}}.$

Ebből számíthatóan

$\displaystyle m_1=\frac1{16},\quad m_2=\frac1{64},\quad \ldots \quad m_k=\frac1{4^{k+1}}.$

A kivágott lemez tömege:

$\displaystyle M_1=1-m_1=\frac{15}{16},\quad M_2=1-m_1-m_2=\frac{59}{64},$

és általában

$\displaystyle M_k=1-\sum_{i=1}^k m_k=\frac1{12}\left(11+\frac1{4^k}\right).$

Szükségünk lesz még az $\displaystyle x_k$ távolságokra is.

$\displaystyle x_1=r_1=\frac14, \quad x_2=2r_1+r_2=\frac58,\qquad \ldots\qquad x_k=1-3r_k=1-\frac3{2^{k+1}}.$

Jelöljük $\displaystyle s_k$-val a $\displaystyle k$ lyukat tartalmazó maradék idom tömegközéppontjának az eredeti kör középpontjától mért távolságát $\displaystyle s_k$-val. A feladatunk $\displaystyle s_1$, $\displaystyle s_2$ és a nagyon nagy $\displaystyle k$-hoz tartozó $\displaystyle s_k \rightarrow s^*$ értékének meghatározása.

Helyezzük (gondolatban) a lyukas idomot vízszintes helyzetben egy, az eredeti kör középpontján átmenő és a feladat ábráján bejelölt sugárra merőleges tengelyre. Az idom jobbra el fog billenni, hiszen $\displaystyle M_kgs_k$ forgatónyomaték hat rá. Ha ezt a forgatónyomatékot ki tudjuk számolni, abból már leolvashatjuk $\displaystyle s_k$ értékét is.

Rakjuk vissza (gondolatban) a kivágott kis körlemezeket, és számítsuk ki az eredő forgatónyomatékukat. Ez éppen a lyukas lemez forgatónyomatékával lesz egyenlő, hiszen a tömör körlemez az átmérőjére, mint forgástengelyre nézve egyensúlyban van. Ezek szerint fennáll, hogy

$\displaystyle M_kgs_k=m_1gx_1+m_2gx_2+\quad \ldots\quad m_kgx_k.$

Nem túl nagy $\displaystyle k$-kra $\displaystyle s_k$ ,,nyers erővel'' kiszámolható:

$\displaystyle s_1=\frac{m_1x_1}{M_1}=\frac1{60}\approx 0{,}017,$

$\displaystyle s_2=\frac{m_1x_1+m_2x_2}{M_2}=\frac{13}{472}\approx 0{,}027,$

és így tovább.

Az $\displaystyle m_k$ és $\displaystyle x_k$ mennyiségek fentebb megadott általános képletének ismeretében (a megfelelő mértani sorok összegzésével) a $\displaystyle k\rightarrow\infty$ határesetet is kiszámíthatjuk:

$\displaystyle s^*=\frac{\sum\limits_{i=1}^\infty m_ix_i}{1-\sum\limits_{i=1}^\infty m_i}=\frac{5}{154}\approx 0{,}032.$

Statisztika:

44 dolgozat érkezett.
5 pontot kapott:	Bokor Endre, Dékány Csaba, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Horváth 999 Anikó, Jánosik Áron, Jánosik Máté, Kertész Balázs, Kozák 023 Áron, Ludányi Levente, Nguyễn Đức Anh Quân, Pálfi Fanni, Schäffer Bálint, Selmi Bálint, Sepsi Csombor Márton, Somlán Gellért, Szabó 314 László, Téglás Panna, Toronyi András, Varga Vázsony.
4 pontot kapott:	Fekete András Albert, Fekete Levente, Fiam Regina.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2019. novemberi fizika feladatai