A P. 5171. feladat (2019. november)

P. 5171. Huzalból egyenlő oldalú háromszöget készítettünk, és két csúcsát az ábra szerint áramforráshoz kapcsoltuk. A hozzá vezető vezetékben 10 A erősségű áram folyik. Mekkora a mágneses indukció a háromszög középpontjában? (Az áramkör távol zárul.)

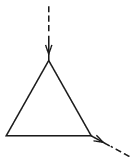
Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2019. december 10-én LEJÁRT.

Megoldás. Ha a be- és kivezetett áram erőssége \(\displaystyle I\), akkor a háromszög oldalai mentén \(\displaystyle \tfrac13I\) és \(\displaystyle \tfrac23I\) erősségű áram folyik, hiszen az összegük \(\displaystyle I\), az arányuk pedig az ellenállásukkal fordított arányában \(\displaystyle 1:2\) kell, hogy legyen.

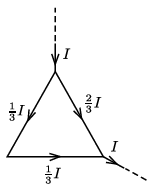
A be- és kivezető ágak árama a háromszög középpontjában nem hoz létre mágneses indukcióvektort, ezt a Biot–Savart-törvény alapján állíthatjuk, vagy az elrendezés szimmetriájára hivatkozva láthatjuk be. A háromszög egy-egy oldala mentén folyó áram által keltett mágneses mező csak integrálszámítással, a középiskolai tananyagot meghaladó matematikai ismeretekkel oldható meg. Anélkül, hogy ezt az utat végigjárnánk, azt állíthatjuk, hogy az egyes oldalak járulékában a mágneses indukció nagysága arányos az áramerősséggel. Tehát az \(\displaystyle \tfrac13I\) erősségű áramot vezető két huzaldarab által együttesen keltett mágneses indukcióvektor éppen ugyanakkora nagyságú, de ellentétes irányú, mint az \(\displaystyle \tfrac13I\) erősségű áram járuléka. (Ez csak a háromszög középpontjára igaz, mert ez a pont egyforma távol van mindhárom oldaltól, és azok felezőmerőlegesén helyezkedik el.)

Ezek szerint az eredő mágneses indukció a háromszög középpontjában nulla.

Statisztika:

29 dolgozat érkezett.
4 pontot kapott:	Sepsi Csombor Márton, Tóth Ábel.
3 pontot kapott:	Fonyi Máté Sándor, Hamar Dávid, Németh Kristóf, Nguyễn Đức Anh Quân.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2019. novemberi fizika feladatai