A P. 5175. feladat (2019. december)

P. 5175. Egy személyautó tengelytávolsága (az első és a hátsó kerekek közötti távolság) 2,6 m, a gépkocsi kerékszélessége (a két első vagy a két hátsó keréknél mérve a futófelületek közepének távolsága az egyenesen haladó autónál) pedig 1,8 m. Frissen behavazott, vízszintes útfelületen egy teljes kört tesz meg az autó. Hány keréknyomot látunk? Mekkora az egyes keréknyomkörök átmérője, ha a legkisebbé 16 m?

Közli: Honyek Gyula, Veresegyház

(4 pont)

A beküldési határidő 2020. január 10-én LEJÁRT.

Megoldás. Az autó hátsó kerekei nem kormányozhatók. A kormányszerkezet csak az első kerekeket fordítja el, méghozzá különböző mértékben, hiszen csak így teljesíthető, hogy a kerekek nyomvonalára merőleges egyenesek ugyanabban a pontban (a körpálya középpontjában) találkozzanak.

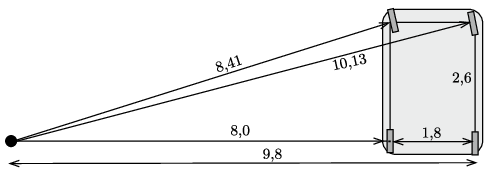
A megadott számokból (a Pitagorasz-tételt felhasználva) kiszámíthatjuk a keréknyomok pályasugarát (lásd az ábrát), és ezekből a körpályák átmérőjét. Ezek rendre (növekvő sorrendben): 16,0 m, 16,8 m, 19,6 m és 20,3 m.

Statisztika:

37 dolgozat érkezett.
4 pontot kapott:	Balázs 825 Ádám , Bekes Barnabás, Bohács Tamás, Csapó Tamás, Endrész Balázs, Jánosik Áron, Kozák Gergely, Lê Minh Phúc, Mucsi Viktor, Németh Kristóf, Pálfi Fruzsina Karina, Perényi Barnabás, Szabados Noémi, Szász Levente, Tanács Kristóf, Téglás Panna, Török 111 László.
3 pontot kapott:	Diószeghy Dániel, Fábián-Kovács Árpád, Horváth Antal, Ludányi Levente, Páhán Anita Dalma, Török 517 Mihály, Vadász Roland.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	6 versenyző.
Nem versenyszerű:	1 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2019. decemberi fizika feladatai