A KöMaL 2019. decemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
K. 639. Egy buszon 53 utas van, férfiak és nők, illetve kislányok és kisfiúk. A nők száma háromszor annyi, mint a kisfiúké, és 10-zel több, mint a kislányoké. Tudjuk továbbá, hogy a férfiak és kisfiúk száma összesen 15. Hány férfi, nő, kisfiú és kislány utazik a buszon?
(6 pont)
K. 640. Egy 5-re végződő kétjegyű számot úgy is négyzetre emelhetünk, hogy a tízesek helyén álló számjegyet megszorozzuk a nála 1-gyel nagyobb számmal, és a szorzat után 25-öt írunk. Indokoljuk meg a módszer helyességét.
(6 pont)
K. 641. Egy konvex négyszög belsejében felveszünk valamennyi pontot. A felvett pontokat egymással és a négyszög csúcsaival úgy kötjük össze egyenes szakaszokkal, hogy az összekötő szakaszoknak a négyszög belsejében ne legyen metszéspontja, és a szakaszok a négyszöget kis háromszögekre és ötszögekre bontsák. (Minden belső pont valamely háromszög vagy ötszög csúcsa.) Előfordulhat-e, hogy a négyszöget pontosan 2019 síkidomra bontottuk fel?
(6 pont)
K. 642. Adjuk meg az összes pozitív egész \(\displaystyle x\) és \(\displaystyle y\) számot, melyekre teljesül, hogy \(\displaystyle x^2-y^2=2019\).
(6 pont)
K. 643. Az
\(\displaystyle \frac{a6bc}{de3fg} \)
törtben a 0 kivételével minden számjegy pontosan egyszer szerepel. Mit jelölhetnek az egyes betűk, ha a tört értéke \(\displaystyle \frac12\)?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
C. 1574. Az ábrán látható metszéspontokra ráírtunk minden egész számot \(\displaystyle 0\)-tól \(\displaystyle 10\)-ig. Ezt követően minden kis háromszögbe beírjuk a csúcsain található számok összegét. Mekkora az így kapott \(\displaystyle 14\) szám összegének lehető legnagyobb, illetve legkisebb értéke?
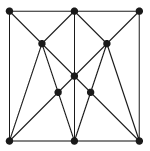
(5 pont)
C. 1575. Határozzuk meg az összes olyan, \(\displaystyle p\), \(\displaystyle q\) pozitív prímekből álló számpárt, amelyre \(\displaystyle 2pq+2p-q=q^2-8\).
Javasolta: Imre Tamás (Marosvásárhely)
(5 pont)
C. 1576. Adott az \(\displaystyle O\) középpontú, egységsugarú kör, valamint a \(\displaystyle P\) pont úgy, hogy \(\displaystyle OP=2\). Tekintsük az egyik \(\displaystyle P\)-n átmenő szelőt, ami a kört az \(\displaystyle M\) és \(\displaystyle N\) pontokban metszi úgy, hogy az \(\displaystyle NP\) szakasz felezőpontja \(\displaystyle M\). Igazoljuk, hogy az \(\displaystyle OMN\) háromszög területe kisebb, mint \(\displaystyle \frac{1}{2}\).
(5 pont)
C. 1577. Egy növekvő, végtelen számtani sorozatról tudjuk, hogy közvetlen egymás utáni tagjai a tízes számrendszerbeli két, illetve háromjegyű
\(\displaystyle \overline{ab},\;\overline{abc},\;\overline{cab} \)
számok (a megadott sorrendben). Hány tagja van ennek a számsorozatnak 1552 és 2020 között?
Javasolta: Bíró Bálint (Eger)
(5 pont)
C. 1578. Két egybevágó téglalap úgy helyezkedik el, hogy a kerületük nyolc pontban metszi egymást. Mutassuk meg, hogy a két téglalap közös részének területe nagyobb a területük felénél.
(5 pont)
C. 1579. Oldjuk meg a valós számok halmazán a következő egyenletet:
\(\displaystyle {(x-11)}^{\log_2 (x-10)}= {(x-11)}^{\log_{\frac12}(x-11)}. \)
Javasolta: Bíró Bálint (Eger)
(5 pont)
C. 1580. Bori véletlenszerűen elhelyez 10 pénzérmét egy sorban az asztalra. Egy lépésben mindig egyszerre két szomszédos érmét fordít át a másik oldalára. Mekkora annak a valószínűsége, hogy Bori nem tudja elérni, hogy valahány lépés után minden érmén a ,,fej'' legyen felül?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
B. 5062. Oldjuk meg a következő egyenletrendszert:
$$\begin{align*} x[x]+y[y] & =1,\\ [x]+[y] & =1. \end{align*}$$(MI&Q)
(3 pont)
B. 5063. Az \(\displaystyle ABC\) háromszögben \(\displaystyle BC<AC\) és az \(\displaystyle ACB\sphericalangle\) derékszög. A \(\displaystyle BC\) átmérőjű kört az \(\displaystyle A\)-ból húzott érintők a \(\displaystyle C\) és \(\displaystyle D\) pontban érintik. Az \(\displaystyle AD\) érintő egyenese a \(\displaystyle BC\) egyenest az \(\displaystyle E\) pontban metszi. A \(\displaystyle BC\) szakasz felezőpontja \(\displaystyle O\). Bizonyítsuk be, hogy a \(\displaystyle DEO\) háromszög területe megegyezik az \(\displaystyle AEB\) háromszög területével.
Javasolta: Bíró Bálint (Eger)
(3 pont)
B. 5064. Az ábrán látható 26 mezőből álló ,,tábla'' hányféleképpen fedhető 13 ,,dominóval''? Egy-egy dominó két szomszédos mezőt fed le. (Az egymásba forgatható megoldásokat különbözőnek tekintjük.)
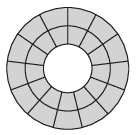
(4 pont)
B. 5065. A hegyesszögű \(\displaystyle ABC\) háromszög köré írt kör középpontja \(\displaystyle O\), az \(\displaystyle O\) pont tükörképe a \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalakra rendre \(\displaystyle O_A\), \(\displaystyle O_B\), illetve \(\displaystyle O_C\). Mutassuk meg, hogy az \(\displaystyle AO_A\), \(\displaystyle BO_B\) és \(\displaystyle CO_C\) egyenesek egy ponton mennek át.
(4 pont)
B. 5066. Harminc diák a ,,Tautologika'' nevű tantárgyból vizsgázik. A diákok egy teremben ülnek, és a tanár egyetlen kérdést tesz fel nekik: ,,Az itt ülő 30 diákból összesen hányan fognak megbukni ezen a vizsgán?'' A diákoknak sorban egy-egy számot kell mondani. Minden egyes válasz elhangzása után a tanár azonnal kihirdeti az eredményt is, ami ,,megfelelt'' vagy ,,megbukott'' lehet.
A hallgatói önkormányzat elérte, hogy a vizsga után egy szakfelügyelő ellenőrizze az eredményeket. Ha van olyan diák, aki helyesen válaszolt, de mégis megbukott, a vizsga összes eredményét érvénytelenítik, és mindenki ,,megfelelt'' minősítést kap.
Van-e a diákoknak olyan stratégiája, ami biztosítja, hogy mindegyikük átmenjen a vizsgán?
(Orosz feladat)
(5 pont)
B. 5067. Az \(\displaystyle ABC\) hegyesszögű háromszög \(\displaystyle AB\) oldalának felezőpontja \(\displaystyle F\), az \(\displaystyle F\)-re illeszkedő \(\displaystyle e\) egyenes felezi \(\displaystyle ABC\) kerületét. Az \(\displaystyle e\) egyenes a \(\displaystyle BC\) és \(\displaystyle CA\) oldalegyeneseket rendre \(\displaystyle D\) és \(\displaystyle E\) pontokban metszi. Mutassuk meg, hogy az \(\displaystyle AB\)-re \(\displaystyle F\)-ben állított merőleges, a \(\displaystyle BC\)-re \(\displaystyle D\)-ben állított merőleges, és a \(\displaystyle CA\)-ra \(\displaystyle E\)-ben állított merőleges egyenesek egy pontban metszik egymást.
(5 pont)
B. 5068. Tegyük fel, hogy \(\displaystyle p\) egy legfeljebb 1998-adfokú polinom, melyre a \(\displaystyle p(1), p(2),\dots,p(2000)\) értékek az \(\displaystyle 1,2,\dots,2000\) számok egy permutációja. Következik-e ebből, hogy a \(\displaystyle p(1)\) és \(\displaystyle p(2000)\) számok az \(\displaystyle 1\) és \(\displaystyle 2000\) valamelyik sorrendben?
(6 pont)
B. 5069. Az \(\displaystyle ABCD\) deltoid szimmetriatengelye \(\displaystyle AC\). Az \(\displaystyle AB\) oldalra \(\displaystyle B\)-ben, és a \(\displaystyle CD\) oldalra \(\displaystyle D\)-ben állított merőlegesek metszéspontja \(\displaystyle M\). Mutassuk meg, hogy \(\displaystyle AMD\sphericalangle=BMC\sphericalangle\).
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2020. január 10-én LEJÁRT. |
A. 764. Egy sokszög egy átlóját szépnek nevezzük, ha végig a sokszög belsejében vagy végig a sokszögön kívül halad. Legyen \(\displaystyle P\) egy olyan \(\displaystyle n\)-szög, amelynek semelyik három csúcsa nem esik egy egyenesre. Bizonyítandó, hogy \(\displaystyle P\)-nek legalább \(\displaystyle \frac32(n-3)\) szép átlója van.
Javasolta: Hujter Bálint (Budapest) és Szűcs Gábor (Szikszó)
(7 pont)
A. 765. Határozzuk meg az összes olyan \(\displaystyle f\colon \mathbb{R}\to\mathbb{R}\) függvényt, amelyre minden \(\displaystyle x,y\in \mathbb{R}\) esetén fennáll a következő egyenlőség:
\(\displaystyle f(x)f(y)-f(x-1)-f(y+1)=f(xy)+2x-2y-4. \)
Javasolta: Dobák Dániel (Budapest)
(7 pont)
A. 766. Legyen \(\displaystyle H\) egy olyan háromszög, amelyben mindhárom oldal és a körülírt kör sugara is egész hosszúságú. Bizonyítandó, hogy
\(\displaystyle a)\) \(\displaystyle H\)-ban a beírt kör sugarának hossza egész;
\(\displaystyle b)\) \(\displaystyle H\) kerületének hossza osztható néggyel;
\(\displaystyle c)\) \(\displaystyle H\) mindhárom oldalának hossza páros.
Javasolta: Nikolai Beluhov (Bulgaria)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

