 |
A P. 5218. feladat (2020. március) |
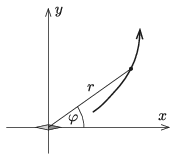
P. 5218. A derékszögű koordináta-rendszer origójában elhelyezett kicsiny, ,,pontszerű'' mágnestű az \(\displaystyle x\) tengely irányába mutat. Egyik mágneses erővonalának egyenlete \(\displaystyle r=r_0\sin^2\varphi\), ahol \(\displaystyle r\) és \(\displaystyle \varphi\) az erővonal egy-egy pontjának ún. polárkoordinátái.
\(\displaystyle a)\) Írjuk fel ennek az erővonalnak az egyenletét \(\displaystyle x\) és \(\displaystyle y\) koordinátákkal kifejezve, ha \(\displaystyle r_0=3\) méter!
\(\displaystyle b)\) Az erővonalnak hol vannak olyan pontjai, ahol a mágneses indukcióvektor iránya merőleges a mágnestűre?
Közli: Radnai Gyula, Budapest
(6 pont)
A beküldési határidő 2020. április 14-én LEJÁRT.
I. megoldás. \(\displaystyle a)\) Mivel a derékszögű koordinátákkal \(\displaystyle r\) és \(\displaystyle \sin\varphi\) így fejezhető ki:
\(\displaystyle r=\sqrt{x^2+y^2}; \qquad \sin\varphi=\frac{y}{\sqrt{x^2+y^2}},\)
az erővonal egyenlete:
\(\displaystyle \sqrt{x^2+y^2}=r_0\frac{y^2}{x^2+y^2},\)
vagyis
| \(\displaystyle (1)\) | \(\displaystyle \left(x^2+y^2\right)^3=r_0^2\,y^4.\) |
\(\displaystyle b)\) A másneses indukcióvektorok az erővonalak érintője irányába mutatnak. Ha ez az irány az \(\displaystyle y\) tengellyel párhuzamos, akkor az erővonal két közeli pontjának \(\displaystyle x\) koordinátája jó közelítéssel megegyezik.
Fejezzük ki az \(\displaystyle x\) koordinátát a \(\displaystyle \varphi\) szög segítségével:
\(\displaystyle x(\varphi)=r\cos\varphi=r_0\sin^2\varphi\,\cos\varphi=r_0(\cos\varphi-\cos^3\varphi).\)
Látszik, hogy érdemes bevezetni a \(\displaystyle \xi\equiv\cos\varphi\) új változót (\(\displaystyle -1\le\xi\le1\)), ezzel kifejezve azt kapjuk, hogy az erővonal pontjaiban
\(\displaystyle x(\xi)=r_0\left(\xi-\xi^3\right).\)
A mágneses indukcióvektor azon pontban (pontokban) merőleges az \(\displaystyle x\) tengelyre, ahol a \(\displaystyle x(\xi)\) függvény egymáshoz nagyon közeli pontokban – jó közelítéssel – ugyanazt az értéket veszi fel:
\(\displaystyle x(\xi+\Delta\xi)\approx x(\xi),\)
vagyis
\(\displaystyle (\xi+\Delta\xi)-(\xi+\Delta\xi)^3\approx \xi- \xi^3.\)
Innen algebrai átalakítások után azt kapjuk, hogy
\(\displaystyle 3\xi^2 =1-3\xi(\Delta\xi)-(\Delta\xi)^2\approx 1, \qquad \text{vagyis}\qquad \xi=\pm \frac{1}{\sqrt{3}}.\)
(A közelítés annál pontosabban teljesül, minél kisebb \(\displaystyle \Delta\xi\).)
Megjegyzés. Ugyanezt az eredményt természetesen a differenciálszámítás formális szabályainak alkalmazásával is megkaphatjuk:
\(\displaystyle x(\xi)'=1-3\xi^2=0 \quad \Rightarrow \quad \xi=\pm \frac{1}{\sqrt{3}}.\)
A mágneses indukcióvektor azon pontban (pontokban) merőleges az \(\displaystyle x\) tengelyre, ahol \(\displaystyle \cos\varphi=\pm \frac{1}{\sqrt{3}}.\) Ez összesen 4 helyen teljesül:
\(\displaystyle \varphi=\pm 54{,}7^\circ, \qquad\text{vagy}\qquad \varphi=\pm 125{,}3^\circ.\)
Ezekben a pontokban
\(\displaystyle r= r_0\sin^2\varphi=r_0\left(1-\xi^2\right)=\frac{2}{3}r_0=2~\text{m}.\)
A megfelelő derékszögű koordináták:
\(\displaystyle x=r\cos\varphi =\pm \frac{2}{3\sqrt{3}}r_0\approx \pm1{,}15~\rm m, \)
\(\displaystyle y=r\sin\varphi=\pm \frac{2\sqrt{2}} {3\sqrt{3}}r_0\approx \pm1{,}63~\rm m. \)
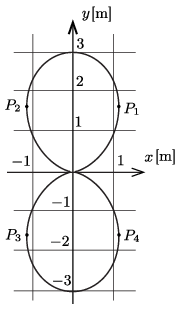
Az \(\displaystyle r_0=3\) m-nek megfelelő mágneses erővonalakon tehát a mágneses indukcióvektor az ábrán látható \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle P_3\) és \(\displaystyle P_4\) pontban merőleges a mágnestű irányára.
II. megoldás. Fejezzük ki az (1) képletből \(\displaystyle x\)-et \(\displaystyle y\) függvényében:
| \(\displaystyle (2)\) | \(\displaystyle x(y)=\sqrt{r_0^{\frac23} \,y^{\frac43}-y^2}.\) |
Ahol ennek a függvénynek a deriváltja nulla, ott lesz a mágneses indukcióvektor merőleges a mágnestűre (vagyis az \(\displaystyle x\) tengelyre). A derivált a differenciálszámítás szabályait követve, esetleg internetes segítséggel számítható ki:
| \(\displaystyle (3)\) | \(\displaystyle \frac{{\rm d}x}{{\rm d}y}= \frac{1}{2\sqrt{r_0^{\frac23} \,y^{\frac43}-y^2}} \left(r_0^{\frac23} \,y^{\frac13}\frac{4}{3}-2y \right)=0,\quad\text{vagyis ha}\quad y^2=\left(\frac23\right)^3r_0^2.\) |
Ezt (2)-be visszahelyettesítve
| \(\displaystyle (4)\) | \(\displaystyle x^2=\frac{1}{3} \left(\frac23r_0\right)^2\) |
adódik. (3)-t (4)-gyel elosztva az
\(\displaystyle \frac{y^2}{x^2}=\tg^2\varphi=2, \qquad \tg\varphi=\pm \sqrt{2},\quad \varphi=\pm 54{,}7^\circ \quad\text{vagy}\quad \varphi=\pm 125{,}3^\circ.\)
Ezeknek a szögeknek az \(\displaystyle r=\tfrac{2}{3}r_0=2~\)m-es távolság felel meg. A megfelelő derékszögű koordináták:
\(\displaystyle x= \pm \frac{2}{3\sqrt{3}}r_0\approx \pm1{,}15~{\rm m}\quad \text{és}\quad y=\pm \frac{2\sqrt{2}} {3\sqrt{3}}r_0\approx \pm1{,}63~\rm m. \)
III. megoldás. Számítógéppel kirajzoltatva az áramvonal (1)-nek megfelelő görbéjét (lásd az I. megoldás ábráját), arról – közelítőleg – leolvashatjuk a kérdéses pontok derékszögű koordinátáit.
IV. megoldás. \(\displaystyle c)\) Mágnességgel foglalkozó szakkönyvekben (pl. Budó Ágoston: Kísérleti fizika II. kötet 26. old.) megtalálható, hogy egy kis méretű (pontszerűnek tekinthető) mágneses dipólus indukcióvektora az \(\displaystyle \boldsymbol r\) helyen így adható meg:
\(\displaystyle {\boldsymbol B}(\boldsymbol r)=\text{állandó}\cdot \frac{3({\boldsymbol m}{\boldsymbol r}){\boldsymbol r}-{\boldsymbol m}\,r^2}{r^5},\)
ahol \(\displaystyle \boldsymbol m\) a dipólus irányába mutató egységvektor.
A mágneses indukció vektora azon a helyen lesz merőleges \(\displaystyle {\boldsymbol m}\)-re, ahol a \(\displaystyle {\boldsymbol B}{\boldsymbol m}\) skalárszorzat nulla, vagyis ahol
\(\displaystyle 3({\boldsymbol m}{\boldsymbol r})^2\equiv 3r^2\cos^2\varphi=r^2,\)
azaz
\(\displaystyle \cos\varphi=\pm \frac{1}{\sqrt{3}}.\)
Ez \(\displaystyle \varphi=\pm 54{,}7^\circ\) és \(\displaystyle \varphi=\pm 125{,}3^\circ\)-nál teljesül, és ezeken a helyeken \(\displaystyle r=\tfrac23 \,r_0=2\) m, továbbá \(\displaystyle x=\pm 1{,}15~{\rm m}\), illetve \(\displaystyle y=\pm 1{,}63~{\rm m}\).
Statisztika:
24 dolgozat érkezett. 6 pontot kapott: Békési Ábel, Bokor Endre, Fekete András Albert, Fiam Regina, Hamar Dávid, Kertész Balázs, Lê Minh Phúc, Ludányi Levente, Nguyễn Đức Anh Quân, Selmi Bálint, Sepsi Csombor Márton, Szabó 314 László, Téglás Panna, Toronyi András, Tóth Ábel, Varga Vázsony, Vass Bence, Viczián Anna. 5 pontot kapott: Bonifert Balázs, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Hung Vo. 2 pontot kapott: 2 versenyző.
A KöMaL 2020. márciusi fizika feladatai
