 |
A P. 5264. feladat (2020. november) |
P. 5264. Egy versenyautó 60 m sugarú, kör alakú tesztpályán álló helyzetből indul. Érintőleges gyorsulása a mozgás első négy másodpercében állandó, nagysága \(\displaystyle 6~\mathrm{m/s}^2\).
\(\displaystyle a)\) Határozzuk meg és ábrázoljuk vázlatosan az idő függvényében, hogy mekkora szögsebességgel forog az autó gyorsulásvektora a menetirányhoz képest!
\(\displaystyle b)\) Mennyi idő múlva lesz ez a szögsebesség a legnagyobb? Mekkora lesz ez a maximális szögsebesség?
Közli: Szabó Endre, Vágfüzes, Szlovákia
(5 pont)
A beküldési határidő 2020. december 15-én LEJÁRT.
I. megoldás. \(\displaystyle a)\) SI-egységeket használva:
– az autó érintőleges gyorsulása \(\displaystyle a_1=6\);
– a pálya sugara: \(\displaystyle r=60\);
– az autó sebessége \(\displaystyle t\) idő elteltével \(\displaystyle v=a_1t=6t\);
– az autó centripetális gyorsulása: \(\displaystyle a_2=\frac{v^2}{r}=0{,}6\,t^2\). Az autó gyorsulásvektora a kör érintőjével
\(\displaystyle \alpha(t)=\arctg\frac{a_2}{a_1}=\arctg(0{,}1\,t^2)\)
szöget zár be. Ennek a szögnek az egységnyi időre vonatkozó megváltozása a keresett
\(\displaystyle \omega(t)= \frac{\Delta\alpha}{\Delta t} \)
szögsebesség.
Számítsuk ki, hogy mennyit változik \(\displaystyle \tg\alpha\) egy kicsiny \(\displaystyle \Delta t\) idő alatt, ha eközben az \(\displaystyle \alpha\) szög \(\displaystyle \Delta\alpha\)-val nagyobb lesz. Mivel \(\displaystyle \tg\alpha=0{,}1\,t^2\), fennáll, hogy
\(\displaystyle \tg(\alpha+\Delta\alpha)-\tg\alpha=0{,}1 (t+\Delta t)^2-0{,}1 t^2.\)
Kicsiny változások esetén érvényes
\(\displaystyle \tg(\Delta\alpha)\approx \Delta\alpha\qquad \text{és}\qquad \Delta t\ll t.\)
Trigonometriai és algebrai átalakítások után kapjuk, hogy ebben a közelítésben
\(\displaystyle \frac{\tg\alpha+\Delta\alpha}{1-\Delta\alpha\cdot \tg\alpha}-\tg\alpha=0{,}2t\,\Delta t+0{,}1(\Delta t)^2,\)
azaz
\(\displaystyle \Delta\alpha\left(1+\tg^2\alpha\right)=\Delta t(0{,}2t+0{,}1t\,\Delta t)(1-\Delta\alpha\,\tg\alpha).\)
Innen kapjuk, hogy a keresett szögsebesség:
\(\displaystyle \omega(t)\approx \frac{\Delta\alpha}{\Delta t}= \frac{0{,}2\,t+0{,}1\Delta t}{1+\tg^2\alpha} (1-\Delta\alpha\cdot\tg\alpha) =\frac{0{,}2\,t}{1+0{,}01\,t^4}.\)
Ha ábrázoljuk az \(\displaystyle \omega(t)\) függvényt, a grafikonról leolvashatjuk, hogy a szögsebességnek \(\displaystyle t=2{,}4\) s közelében maximuma van, és hogy a szögsebesség legnagyobb értéke \(\displaystyle \omega_\text{max}=0{,}36\, \rm s^{-1}\).
Megjegytés. \(\displaystyle \omega(t)\) szélsőértékét deriválással is meghatározhatjuk: A differenciálhányados \(\displaystyle t_0=\sqrt[4]{100/3} \approx 2{,}4\ {\rm s}\) idő elteltével lesz nulla, és \(\displaystyle \omega_\text{max}=\omega(t_0)\approx 0{,}36\,\rm s^{-1}\).
II. megoldás. A feladat elemi úton (a differenciálszámítás felhasználása nélkül) is megoldható. Az autó inerciarendszerbeli \(\displaystyle \boldsymbol a\) gyorsulásvektora az autóhoz rögzített (tehát egyenletes gyorsuló szögsebességgel forgó) \(\displaystyle (X,Y)\) koordináta-rendszerben \(\displaystyle \boldsymbol a=(a_1, a_2)\) módon adható meg (1. ábra), ahol – az I. megoldás elején leírtaknak megfelelően
\(\displaystyle a_1= 6 \qquad \text{és}\qquad a_2=0{,}6\,t^2.\)
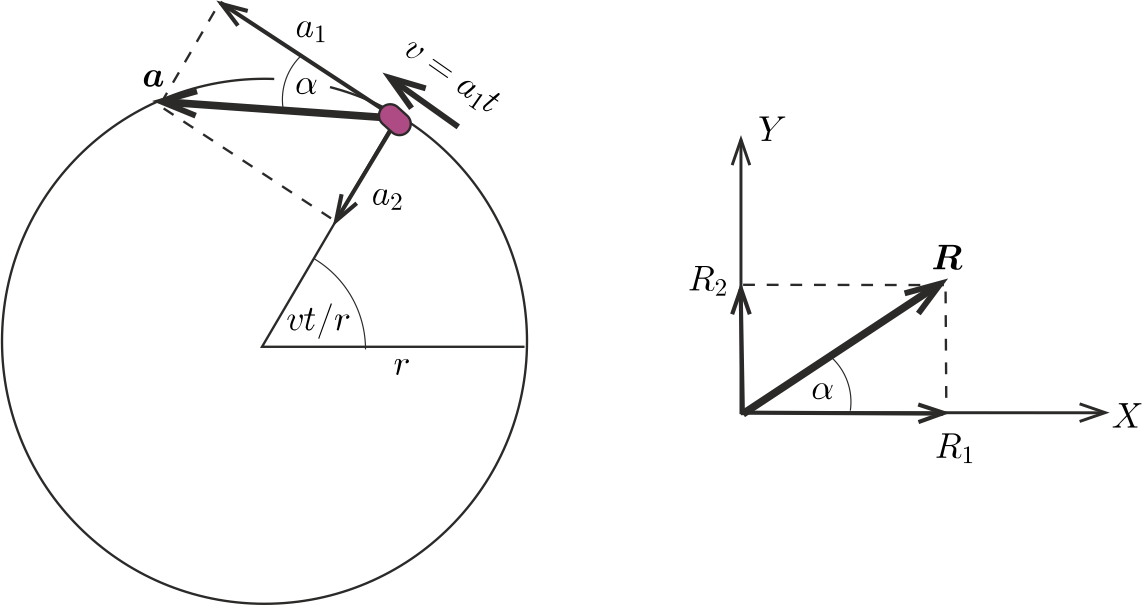
1. ábra
A továbbiakban a gyorsulásvektort \(\displaystyle \boldsymbol R\)-rel, ezen vektor változási sebességét \(\displaystyle \boldsymbol V\)-rel, ez utóbbi változási sebességét (vagyis a \(\displaystyle \boldsymbol R\) gyorsulását) \(\displaystyle \boldsymbol A\)-val fogjuk jelölni. (Az átjelölés oka: el akarjuk kerülni a \(\displaystyle \boldsymbol V\) vektornak és az autó \(\displaystyle \boldsymbol v\) sebességvektorának, valamint \(\displaystyle \boldsymbol A\)-nak és \(\displaystyle \boldsymbol a\)-nak esetleges összetévesztését.) Ennek megfelelően írhatjuk, hogy
\(\displaystyle R_1= 6, \qquad R_2=0{,}6\,t^2.\)
Ráismerhetünk, hogy ezek éppen egy olyan test koordinátái, amely az \(\displaystyle Y\) tengely irányában egyenletesen gyorsuló mozgást végez \(\displaystyle 1{,}2\) nagyságú gyorsulással. Így tehát
\(\displaystyle V_1= 0, \qquad V_2=1{,}2\,t,\)
és
\(\displaystyle A_1= 0, \qquad A_2=1{,}2.\)
Az \(\displaystyle \boldsymbol R\) vektor nagyságát jelölje \(\displaystyle R\), az autó haladási irányával (vagyis az \(\displaystyle X\) tengellyel) bezárt szöge pedig legyen \(\displaystyle \alpha\). Ennek megfelelően
| \(\displaystyle (1)\) | \(\displaystyle R=\sqrt{R_1^2+R_2^2}=6\sqrt{1+0{,}01\,t^4},\) |
továbbá
| \(\displaystyle (2)\) | \(\displaystyle \cos\alpha=\frac{R_1}{R}=\frac{1}{\sqrt{1+0{,}01\,t^4}}\) |
és
\(\displaystyle \sin\alpha=\frac{R_2}{R}=\frac{0{,}1\,t^2}{\sqrt{1+0{,}01\,t^4}.} \)
a) A \(\displaystyle \boldsymbol V\) vektort nemcsak az \(\displaystyle X,Y\) koordinátákkal, hanem \(\displaystyle \boldsymbol R\) irányú \(\displaystyle V_\text{rad}\) ,,radiális'' és arra merőleges \(\displaystyle V_\text{tan}\) ,,tangenciális'' komponensekkel is jellemezhetjük (2. ábra).
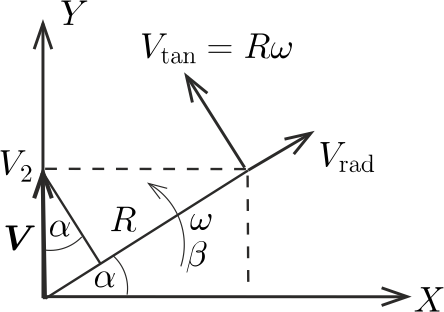
2. ábra
Az ábráról leolvashatjuk, hogy
\(\displaystyle V_\text{rad}=V_2\sin\alpha={1{,}2\,t}\, \frac{0{,}1\,t^2}{\sqrt{1+0{,}01\,t^4}}=\frac{0{,}12\,t^3}{\sqrt{1+0{,}01\,t^4}},\)
valamint
| \(\displaystyle (3)\) | \(\displaystyle V_\text{tan}=R\omega=V_2\cos\alpha=\frac{1{,}2\,t }{\sqrt{1+0{,}01\,t^4}},\) |
tehát a kérdéses szögsebesség:
| \(\displaystyle (4)\) | \(\displaystyle \omega=\frac{V_\text{tan}}{R}=\frac{0{,}2\,t }{ 1+0{,}01\,t^4} .\) |
b) A fentebb leírtakhoz hasonlóan járhatunk el az \(\displaystyle \boldsymbol A\) vektorral is (3. ábra).
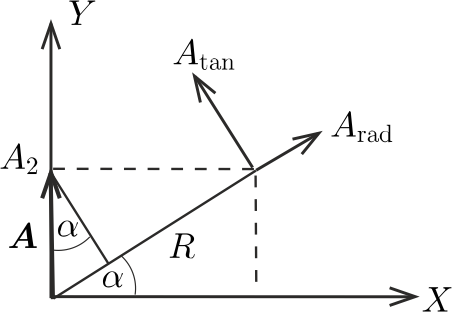
3. ábra
Itt azonban figyelembe kell vegyük, hogy a radiális és a tangenciális komponensek, valamint az \(\displaystyle (A_1,A_2)\) komponensek közötti kapcsolat a forgásból származó extra tagokat is tartalmaz:
\(\displaystyle A_\text{rad}= \frac{\Delta V_\text{rad}}{\Delta t}-R\omega^2, \)
ahol a jobb oldal második tagja a centripetális gyorsulás, valamint
| \(\displaystyle (5)\) | \(\displaystyle A_\text{tan}=R\beta+2V_\text{rad}\,\omega, \) |
ahol a jobb oldal második tagja a Coriolis-gyorsulás.
Megjegyzás. Egy \(\displaystyle m\) tömegű test forgó koordináta-rendszerbeli mozgásegyenletében a centrifugális erő a centripetális gyorsulás \(\displaystyle (-m)\)-szerese, a Coriolis-erő pedig a Coriolis-gyorsulás \(\displaystyle (-m)\)-szerese. (Lásd pl. a Négyjegyű függvénytáblázatokban a tehetetlenségi erők képleteit.)
Abban a \(\displaystyle t_0\) pillanatban, amikor az \(\displaystyle \omega\) szögsebesség a legnagyobb, a \(\displaystyle \beta\) szöggyorsulás nulla, így (1-5) egyenletekből következően
\(\displaystyle A_2\,\cos\alpha=2V_\text{rad}\,\omega,\)
azaz
\(\displaystyle {1{,}2}\cdot\frac{1}{\sqrt{1+0{,}01\,t_0^4}}=2\cdot\frac{0{,}12\,t_0^3}{\sqrt{1+0{,}01\,t_0^4}}\cdot\frac{0{,}2\,t_0 }{\ 1+0{,}01\,t_0^4} .\)
Innen
\(\displaystyle 0{,}04\,t_0^4=1+0{,}01\,t_0^4,\qquad \text{azaz}\qquad t_0=\root 4 \of {\frac{1}{0{,03}}}\approx 2{,}4\ \rm [s], \)
a szögesbesség legnagyobb értéke pedig
\(\displaystyle \omega_\text{max}=\omega(t_0)=\frac{3}{20}\root 4 \of {\frac{100}{3}}\approx 0{,}36\ \left[\rm s^{-1}\right].\)
Statisztika:
40 dolgozat érkezett. 5 pontot kapott: Bonifert Balázs, Fekete András Albert, Fey Dávid, Fonyi Máté Sándor, Gurzó József, Horváth 999 Anikó, Jánosik Máté, Juhász Márk Hunor, Kertész Balázs, Kovács Kinga, Ludányi Levente, Molnár-Szabó Vilmos, Németh Kristóf, Sas 202 Mór, Schäffer Bálint, Selmi Bálint, Simon László Bence, Somlán Gellért, Takács Bendegúz, Téglás Panna, Tóth Ábel, Varga Vázsony. 4 pontot kapott: Koleszár Benedek, Köpenczei Csanád, Magyar Gábor Balázs, Mihalik Bálint, Molnár 123 Barnabás, Toronyi András. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. novemberi fizika feladatai
