 |
A P. 5287. feladat (2021. január) |
P. 5287. Van három ellenállásunk, rendre 1 ohm, 2 ohm, 3 ohm értékűek. Mindegyiken a megengedett legnagyobb teljesítmény 1 watt lehet. A három ellenállást minden lehetséges módon összekapcsoljuk úgy, hogy mindig mindegyiken folyhasson áram.
\(\displaystyle a)\) Milyen határok között változhat a legnagyobb megengedett összteljesítmény?
\(\displaystyle b)\) Melyik kapcsolás esetén lehet a legnagyobb összteljesítmény pontosan 2 watt?
Közli: Varga Zsuzsa, Szeged
(4 pont)
A beküldési határidő 2021. február 18-án LEJÁRT.
Megoldás. A három ellenállást nyolcféle módon kapcsolhatjuk össze.
\(\displaystyle (a)\) Mindhárom ellenállást sorosan kapcsoljuk (1.a) ábra). Ekkor a rajtuk átfolyó áram erőssége egyforma, tehát a teljesítményük: \(\displaystyle P_1=I^2\cdot 1~\Omega\), \(\displaystyle P_2=I^2\cdot 2~\Omega\) és \(\displaystyle P_3=I^2\cdot 3~\Omega\). (Az egyes elemekhez tartozó fizikai mennyiségeket az ellenállásuk ohmban mért értékével megegyező indexszel jelöljük.) Látható, hogy a legnagyobb teljesítmény \(\displaystyle P_3\), és az akkor egyezik meg 1 wattal, ha \(\displaystyle I^2=\frac13\). (Az SI mértékegységeket a továbbiakban nem írjuk ki.) Ekkor
\(\displaystyle (a)\text{~eset:} \hskip 2cm P_1=\frac13=0{,}33,\qquad P_2=\frac{2}{3}=0{,}67,\qquad P_3= 1{,}00, \qquad \sum_{i=1}^3 P_i=2{,}0~\rm watt.\)
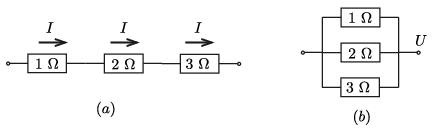
1. ábra
\(\displaystyle (b)\) A három ellenállást párhuzamosan kapcsoljuk, és valamekkora \(\displaystyle U\) feszültséget kötünk rájuk (1.b) ábra). Mivel a rájuk eső feszültség ugyanakkora, a teljesítmények: \(\displaystyle P_1=U^2,\) \(\displaystyle P_2=U^2/2\) és \(\displaystyle P_3=U^2/3\). Látható, hogy a legnagyobb teljesítmény \(\displaystyle P_1\), és az akkor egyezik meg 1 wattal, ha \(\displaystyle U^2=1\). Ekkor
\(\displaystyle (b)\text{~eset:} \hskip 2cm P_1=1{,}00,\qquad P_2=\frac12=0{,}50,\qquad P_3=\frac13=0{,}33, \qquad \sum_{i=1}^3 P_i=1{,}83~\rm watt.\)
\(\displaystyle (c)\) Kapcsolhatunk két ellenállást sorosan, és a harmadikat velük párhuzamosan. Ezt háromféleképpen tehetjük meg (2.ábra).

2. ábra
Tekintsük először a \(\displaystyle (c_1)\) kapcsolást. Az 1 ohmos ellenálláson \(\displaystyle U\), a másik kettőn \(\displaystyle U/5\) erősségű áram folyik. Ennek megfelelően a teljesítmények:
\(\displaystyle P_1=U^2, \qquad P_2=2\left(\frac{U}{5}\right)^2=\frac{2}{25}U^2, \qquad P_3=\frac{3}{25}U^2.\)
Ezek közül \(\displaystyle P_1\) a legnagyobb, és \(\displaystyle U^2=1\) esetén éppen 1 watt. Ezek szerint
\(\displaystyle (c_1)\text{~eset:} \hskip 2cm P_1=1{,}00,\qquad P_2=\frac2{25}=0{,}08,\qquad P_3 =\frac3{25}=0{,}12,\qquad \sum_{i=1}^3 P_i=1{,}20~\rm watt.\)
Hasonló számítással kapjuk, hogy
\(\displaystyle (c_2)\text{~eset:} \hskip 2cm P_1 =1{,}00,\qquad P_2=\frac18=0{,}125,\qquad P_3= \frac38=0{,}375,\qquad \sum_{i=1}^3 P_i=1{,}5~\rm watt,\)
és végül
\(\displaystyle (c_3)\text{~eset:} \hskip 2cm P_1 =1{,}00,\qquad P_2=\frac13=0{,}33,\qquad P_3= \frac23=0{,}675,\qquad \sum_{i=1}^3 P_i=2{,}0~\rm watt,\)
\(\displaystyle (d)\) Kapcsolhatunk két ellenállást párhuzamosan, és a harmadikat velük sorosan. Ezt is háromféleképpen tehetjük meg (3.ábra).
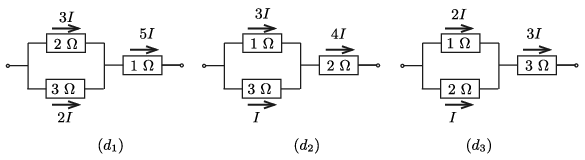
3. ábra
Tekintsük a \(\displaystyle (d_1)\) kapcsolást. A 2 ohmos és a 3 ohmos ellenállásokon folyó áramok aránya \(\displaystyle 3:2\), ekkor lesz ugyanis a rájuk eső feszültség ugyanakora. Legyen ez a kér áramerősség \(\displaystyle 3I\) és \(\displaystyle 2I\), a harmadik ellenálláson ekkor \(\displaystyle 5I\) erősségű áram folyik. Az egyes teljesítmények:
\(\displaystyle P_1=25\,I^2,\qquad P_2=3\cdot (2I)^2=12\,I^2, \qquad P_3=2\cdot (3I)^2=18\,I^2.\)
Ezek közül \(\displaystyle P_1\) a legnagyobb, és \(\displaystyle I^2=\frac{1}{25}\) esetén egyezik meg 1 wattal. A megfelelő teljesítmények ekkor:
\(\displaystyle (d_1)\text{~eset:} \hskip 2cm P_1=1{,}00,\qquad P_2=\frac{18}{25}=0{,}72,\qquad P_3 =\frac{12}{25}=0{,}48,\qquad \sum_{i=1}^3 P_i=2{,}2~\rm watt.\)
Hasonló számítással kapjuk, hogy
\(\displaystyle (d_2)\text{~eset:} \hskip 2cm P_1=\frac{9}{32}=0{,}28,\qquad P_2=1{,}00,\qquad P_3 =\frac{3}{32}=0{,}09,\qquad \sum_{i=1}^3 P_i=1{,}37~\rm watt,\)
és
\(\displaystyle (d_3)\text{~eset:} \hskip 2cm P_1=\frac4{27}=0{,}15\qquad P_2=\frac{2}{27}=0{,}07,\qquad P_3 =1{,}00,\qquad \sum_{i=1}^3 P_i=1{,}22~\rm watt.\)
Összefoglalva megállapíthatjuk, hogy három ellenállás megengedett összteljesítménye 1,2 W és 2,2 W között változhat, és két kapcsolásnál is éppen 2 W az értéke.
Statisztika:
42 dolgozat érkezett. 4 pontot kapott: Antalóczy Szabolcs, Biebel Botond, Dékány Csaba, Dózsa Levente, Hauber Henrik, Horváth 999 Anikó, Juhász Júlia, Juhász Márk Hunor, Korom Lili, Kovács Kinga, Ludányi Levente, Perényi Barnabás, Puskás Attila, Schmercz Blanka, Somlán Gellért, Szász Levente. 3 pontot kapott: Albert Máté, Bálint Máté, Barta Gergely, Beke Bálint, Gábriel Tamás, Horváth 221 Zsóka, Horváth Antal, Kelecsényi Levente , Köpenczei Csanád, Mozolai Bende Bruno, Németh Kristóf, Szabó Márton, Takács Dóra, Tanner Norman, Tuba Balázs. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2021. januári fizika feladatai
