A P. 5289. feladat (2021. január)

P. 5289. Egy transzmissziós, nagy felbontású optikai rácsra, melynek rései függőlegesen állnak, párhuzamos, monokromatikus fénynyalábot bocsátunk. Kísérletünkben a fénynyaláb merőleges az optikai rácsra, és a rácson való áthaladás után első rendben $\displaystyle 30^\circ$-kal térül el jobbra is és balra is. Ezután a rácsot a középső rés mint tengely körül $\displaystyle 30^\circ$-kal elforgatjuk. Milyen irányokban lép ki most fénynyaláb a rácsból?

Közli: Radnai Gyula, Budapest

(5 pont)

A beküldési határidő 2021. február 18-án LEJÁRT.

Megoldás. A szokásos elrendezésben, amikor a fénynyaláb merőlegesen érkezik a rácsra, az $\displaystyle n$-edrendű elhajlási maximum szögét a

$\displaystyle \sin\alpha=n\frac{\lambda}{d}$

egyenlet határozza meg ($\displaystyle n=0, \pm1, \ldots$). Mivel most $\displaystyle n=\pm 1$-nél $\displaystyle \alpha=\pm 30^\circ$, a rácsállandó a fény hullámhosszának kétszerese: $\displaystyle d=2\lambda$. Ilyen nagy felbontású rács elkészítésének nincs elvi akadálya, de a tényleges megvalósítása nagyon nehéz lenne. Ennél a rácsnál a másodrendű (és annal magasabbrendű) elhajlási maximumok nem alakulhatnak ki, hiszen már $\displaystyle n=\pm 2$ esetén is $\displaystyle \alpha=\pm90^\circ$ lenne, vagyis a fény ,,súrolná'' a rács síkját. Emellett a nagyon finom rácsnál a rések szélessége szükségszerűen összemérhető a hullámhosszal, és az egyes rések jobb- és balszéléről érkező hullámok is részben vagy teljesen kioldhatják egymást.

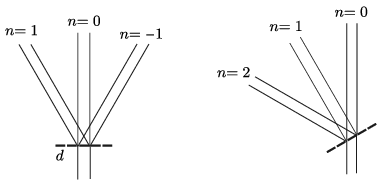
Ha a rácsot $\displaystyle \alpha=30^\circ$-kal elforgatjuk, akkor az egymás melletti résekre eső hullámok útkülönbsége éppen $\displaystyle \lambda$. Eszerint a hullámok éppen olyan fázisban indulnak ki a résekből, mint az elfordítás nélküli esetben. Emiatt az egymást erősítő hullámoknak a rácshoz viszonyított iránya változatlan marad, vagyis az elhajlási kép is a ráccsal együtt $\displaystyle 30^\circ$-kal elfordul.

Statisztika:

18 dolgozat érkezett.
5 pontot kapott:	Fekete András Albert, Fey Dávid, Gurzó József, Kertész Balázs, Koleszár Benedek, Ludányi Levente, Sas 202 Mór, Téglás Panna, Toronyi András, Tóth Ábel, Varga Vázsony.
4 pontot kapott:	Bubics Gergely Dániel, Horváth 999 Anikó.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2021. januári fizika feladatai