 |
A P. 5323. feladat (2021. április) |
P. 5323. Az ábrán látható ellenállásrendszer \(\displaystyle A\) pontjában \(\displaystyle I = 40\) mA erősségű elektromos áram be-, a \(\displaystyle B\) csúcsnál kifolyik.
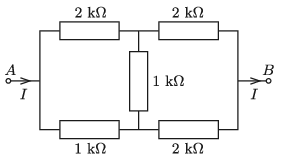
\(\displaystyle a)\) Mekkora elektromos áram folyik az egyes ellenállásokon?
\(\displaystyle b)\) Mekkora az elektromos teljesítmény az egyes ellenállásokon?
\(\displaystyle c)\) Mekkora egyetlen ellenállással lehetne helyettesíteni ezt az ellenállásrendszert?
Közli: Simon Péter, Pécs
(4 pont)
A beküldési határidő 2021. május 17-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Jelöljük a felső ágban folyó áramok erősségét \(\displaystyle xI\) és \(\displaystyle yI\) módon. A többi ágban ( Kirchhoff csomóponti törvényét figyelembe véve) az 1. ábra jelöléseinek megfelelő áramok folynak.
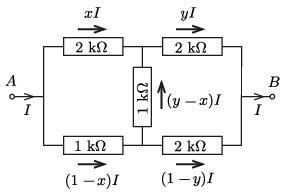
1. ábra
A Kirchhoff-féle huroktörvény szerint:
\(\displaystyle 2x-(y-x)-(1-x)=0\qquad\text{és}\qquad (y-x)+2y-2(1-y)=0.\)
Ennek az egyenletrendszernek a megoldása:
\(\displaystyle x=\frac{7}{19}\qquad\text{és}\qquad y=\frac{9}{19},\)
vagyis az egyes ellenállásokon folyó áramok a 2. ábrán jelölt értékek (\(\displaystyle I=40\) mA).
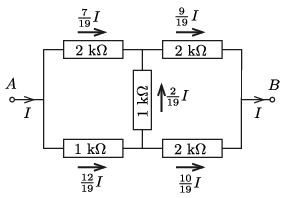
2. ábra
\(\displaystyle b)\) A teljesítmények a \(\displaystyle P=I^2R\) összefüggés szerint számíthatók (3. ábra):
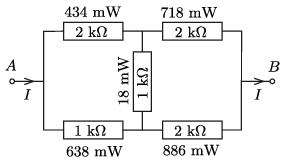
3. ábra
\(\displaystyle c)\) Az 5 ellenállás összteljesítménye \(\displaystyle P=2{,}69\) W. Ha az eredő ellenállás \(\displaystyle R\), akkor \(\displaystyle P=I^2R,\) vagyis
\(\displaystyle R=\frac{2{,}69~\rm W}{(40~\rm mA)^2}\approx 1{,}68~\rm k\Omega.\)
Ugyanezt az eredményt delta-csillag átalakítással is megkaphatjuk: \(\displaystyle R=\tfrac{32}{19}~\rm k\Omega\approx 1{,}68~\rm k\Omega.\)
Statisztika:
38 dolgozat érkezett. 4 pontot kapott: Antalóczy Szabolcs, Biebel Botond, Dóra Márton, Dózsa Levente, Hauber Henrik, Horváth Antal, Jirkovszky-Bari László, Kovács Kinga, Kozák Gergely, Ludányi Levente, Mócza Tamás István, Mozolai Bende Bruno, Páhán Anita Dalma, Selmi Bálint, Somlán Gellért, Téglás Panna, Toronyi András, Török 111 László, Varga Vázsony, Viczián Máté. 3 pontot kapott: Albert Máté, Horváth 999 Anikó, Schmercz Blanka, Strinyi Péter, Szabó Márton. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2021. áprilisi fizika feladatai

