 |
A P. 5372. feladat (2021. december) |
P. 5372. Egy rúdinga (egyik végénél felfüggesztett homogén rúd) szabad lengéseinek körfrekvenciája \(\displaystyle \omega\). Állandósult állapotban mekkora amplitúdójú rezgéseket végez a rúd alsó végpontja, ha az inga felfüggesztési pontját vízszintes irányban \(\displaystyle x(t) = A\cos {(2\omega t)}\) időfüggésű kitéréssel mozgatjuk? (A közegellenállás kicsi, de nem teljesen elhanyagolható, továbbá \(\displaystyle A\omega ^2\ll g\).)
Közli: Vigh Máté, Biatorbágy
(6 pont)
A beküldési határidő 2022. január 17-én LEJÁRT.
Megoldás. A szabad lengések körfrekvenciájából kiszámíthatjuk, hogy a fizikai inga \(\displaystyle \ell\) hossza és az \(\displaystyle \omega\) körfrekvencia közötti kapcsolat
\(\displaystyle T=2\pi\sqrt{ \frac{\frac{1}{3}m\ell^2}{mg\frac{\ell}{2}}},\)
ahonnan
| \(\displaystyle (1)\) | \(\displaystyle \omega=\frac{2\pi}{T}=\sqrt{\frac{3g}{2\ell}},\qquad \text{vagyis}\qquad \ell=\frac{3g}{2\omega^2}.\) |
(A megadott \(\displaystyle A\omega^2\ll g\) feltétel szerint \(\displaystyle A\ll \ell\), vagyis az inga \(\displaystyle \varphi\) szögkitérése feltehetően nagyon kicsi marad, és így érvényes, hogy \(\displaystyle \sin\varphi\approx \varphi\), valamint \(\displaystyle \cos\varphi\approx 1\).)
Megjegyzés. Kezdetben, amikor a rúd felső végpontját mozgatni kezdjük, a rúd szögkitérése nagy, akár \(\displaystyle 90^\circ\)-os is lehet. Ez azonban a közegellenállás miatt (akármilyen kicsi is az) idővel lecsillapodik, tehát az állandósult állapotban már kicsivé válik.
Jelöljük az \(\displaystyle m\) tömegű rúdra annak felfüggesztési pontjában ható vízszintes erőt \(\displaystyle F(t)\)-vel, az inga tömegközéppontjának vízszintes irányú elmozdulását \(\displaystyle y(t)\)-vel, a tömegközéppont pillanatnyi gyorsulását pedig \(\displaystyle a_y(t)\)-vel. (A vízszintes koordináta kezdőpontjának válasszuk a felső végpont rezgésének középpontját.) Az inga szögkitérése
\(\displaystyle \varphi(t)= \frac{2}{\ell}(y-x),\)
a szöggyorsulása pedig
\(\displaystyle \beta(t)=\frac{2}{\ell}\left[a_y(t)+4A\omega^2\cos(2\omega t)\right].\)
(Az egyes mennyiségek irányítását az ábrán látható módon értelmezzük.)
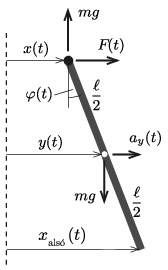
A rúdinga tömegközéppontjának függőleges irányú gyorsulása kis kitérések esetén – jó közelítéssel – nulla, így a felfüggesztési pontban függőlegesen felfelé ható erő \(\displaystyle mg\) nagyságú.
A rúd tömegközéppontjának (vízszintes irányú) mozgásegyenlete:
| \(\displaystyle (2)\) | \(\displaystyle F(t)=ma_y(t),\) |
a tömegközéppont körüli forgómozgásának egyenlete pedig
| \(\displaystyle (3)\) | \(\displaystyle -F(t) \frac{\ell}{2}-mg\left[y(t)-A\cos(2\omega t)\right]=\frac{1}{12}m\ell^2\cdot \frac{2}{\ell} \left[a_y(t)+4A\omega^2\cos(2\omega t)\right].\) |
Megjegyzés. A forgómozgás (3) egyenlete akkor is helyes, ha a tömegközéppont gyorsul. Más gyorsuló pontokra felírt hasonló egyenlet azonban hibás eredményre vezethet (lásd a ,,Merev testek mozgásegyenletei'' című cikket a honlapon, a fizika cikkek között az ,,Ami a tankönyvekből kimaradt, de a versenyzőknek hasznos lehet'' részben).
Az (1), (2) és (3) egyenletekből (\(\displaystyle \ell\) és \(\displaystyle F(t)\) kiküszöbölése után) kapjuk, hogy
\(\displaystyle a_y(t)+\omega^2y(t)=0. \)
Ez egy \(\displaystyle \omega\) körfrekvenciájú harmonikus rezgőmozgás egyenlete, amelynek megoldása
\(\displaystyle y(t)=K \cos\omega(t-t_0).\)
A \(\displaystyle K\) és a \(\displaystyle t_0\) állandókat a rúd középpontjának kezdeti helyzete és a kezdeti sebessége határozza meg.
A \(\displaystyle K\) amplitúdó – ha még a gyenge csillapítást is figyelembe vesszük – fokozatosan csökken, és elegendően hosszú idő múlva (vagyis az állandósult állapotban) nullává válik. Ebből az is következik, hogy az állandósult állapotban \(\displaystyle F(t)\equiv 0\). Mondhatjuk, hogy a kényszerrezgést végző rendszer – a csekély csillapítás miatt – fokozatosan ,,elfelejti'' a kezdőállapotát, és az állandósult állapotban a rezgés (lengés) menete a kezdeti adatoktól függetlenül mindig ugyanolyan lesz.
A rúd közepe tehát a rúdinga mozgása során – jó közelítéssel – mozdulatlan marad, és a felső végpontjának mozgatásához nincs szükség külső erőre. (Ez utóbbi állítás csak csillapításmentes esetben igaz. Ha a közegellenállás egy kicsi, de nem nulla csillapítást jelent, akkor a külső erő munkájának kell ellensúlyoznia a közegellenállásból adódó kicsiny energiaveszteséget.)
A rúd alsó végpontjának elmozdulása
\(\displaystyle x_\text{alsó}(t)=-x(t)=-A\cos(2\omega t).\)
A rúd alja tehát a felső végponttal azonos amlitúdójú, de azzal ellentétes fázisú, \(\displaystyle 2\omega\) körfrekvenciájú harmonikus rezgómozgást végez.
Statisztika:
6 dolgozat érkezett. 5 pontot kapott: Gábriel Tamás. 4 pontot kapott: 4 versenyző.
A KöMaL 2021. decemberi fizika feladatai
