 |
A P. 5390. feladat (2022. február) |
P. 5390. Az ábrán látható \(\displaystyle R\) sugarú, vékony falú, töltetlen fémgömbhéj középpontjában egy kicsiny, \(\displaystyle p\) dipólmomentumú elektromos dipólus helyezkedik el. Határozzuk meg a gömbhéj belső felületén lévő \(\displaystyle A\) és \(\displaystyle B\) pontokban a felületi töltéssűrűséget! Adjuk meg a fémgömbhéj külső felületén lévő töltéssűrűséget is!
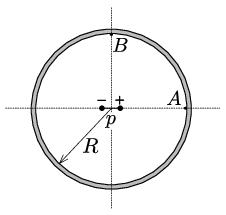
(Útmutatás: Alkalmazhatjuk a gömbi tükörtöltés módszerét. Hasznos lehet még a dipólus elektromos terének ismerete az ún. Gauss-féle főhelyzetekben.)
Közli: Szász Krisztián, Budapest
(6 pont)
A beküldési határidő 2022. március 16-án LEJÁRT.
I. megoldás. Az elektromos dipólust két olyan, \(\displaystyle \pm q\) töltésű, pontszerű testnek gondolhatjuk, amelyek távolsága \(\displaystyle 2\epsilon\ll R\) és \(\displaystyle 2\epsilon q=p\). A dipólus elektromos tere a fémfelületen töltésátrendeződést indít el, ami mindaddig tart, amíg az eredő elektromos tér mindenhol merőleges nem lesz a fémfelületre.
A gömbi tükörtöltés módszere szerint az eredő elektromos tér a gömbhéj belsejében olyan, mintha a dipólus töltésein kívül még két másik elektromos töltés helyezkedne el a gömbhéjon kívül. Ezek töltése \(\displaystyle Q=\mp q\frac{R}{\epsilon}\), távolságuk pedig a gömbhéj középpontjától \(\displaystyle \frac{R^2}\epsilon\) (lásd az ábrát).
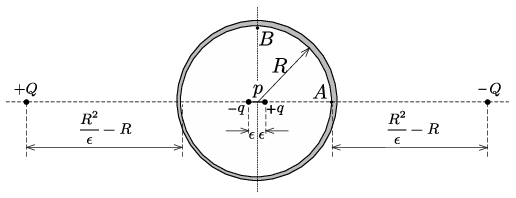
1. ábra
A fém gömbhéj falában nincs elektromos tér, és a gömbhéjon kívül is nulla a térerősség, hiszen a dipólus össztöltése nulla, és a gömbhéj is töltetlen. Így – a fluxustörvény szerint – a gömbhéj külső felületén az elektromos töltéssűrűség mindenhol nulla.
A gömbhéj belsejében az elektromos térerősséget a dipólus és a két tükörtöltés együttesen határozza meg. A felületi töltéssűrűség – a fluxustörvény szerint – a felületnél mérhető elektromos térerősség \(\displaystyle {\varepsilon_0}\)-szorosa.
A \(\displaystyle B\) pontban a \(\displaystyle \pm q\) és \(\displaystyle \mp Q\) töltéspár szimmetriája miatt az eredő térerősség sugár irányú komponense nulla, így a \(\displaystyle B\) pontban a felületi töltéssűrűség: \(\displaystyle \sigma_B=0\).
Számítsuk ki az eredő elektromos térerősséget az \(\displaystyle A\) pontban! (Kihasználjuk, hogy \(\displaystyle \epsilon\ll R\), hogy a gömbhéjba befelé mutató irányt tekintjük pozitívnak.)
\(\displaystyle E_A=\frac{q}{4\pi\varepsilon_0}\left( \frac{1}{(R-\epsilon)^2}-\frac{1}{(R+\epsilon)^2}\right)+ \frac{Q}{4\pi\varepsilon_0}\left(\frac{1}{\left( {R^2}/{\epsilon}+R\right)^2} +\frac{1}{\left( {R^2}/{\epsilon}-R\right)^2} \right)\approx \frac{1}{4\pi\varepsilon_0}\frac{6 \epsilon q}{R^3}=\frac{1}{4\pi\varepsilon_0}\frac{3p}{R^3}.\)
Innen következik, hogy a felületi töltéssűrűség az \(\displaystyle A\) pontban:
\(\displaystyle \sigma_A= -{\varepsilon_0}{E_A}=-\frac{3p}{4\pi R^3}.\)
II. megoldás. Ismerjük, vagy kézikönyvekben megtalálhatjuk, hogy az elektromos térerősség-vektor az ún. Gauss-féle főhelyzetekben, a dipólustól \(\displaystyle R\) távolságban:
\(\displaystyle {\boldsymbol E}_A^\text{(dipól)}=2\cdot\frac{1}{4\pi\varepsilon_0 R^3}{\boldsymbol p}=2{\boldsymbol E}_0,\)
illetve
\(\displaystyle {\boldsymbol E}_B^\text{(dipól)}=-\frac{1}{4\pi\varepsilon_0 R^3}{\boldsymbol p}=-{\boldsymbol E}_0.\)
A dipólus elektromos tere önmagában nem merőleges a fém gömbhéj felületére, ezért nem írja le helyesen a feladatban szereplő tényleges erőteret. De ha hozzáadunk a dipólus teréhez egy megfelelően választott homogén elektromos teret, akkor az eredő a gömbhéj belső felületénél mindenhol sugár irányú lesz, vagyis merőleges a fémfelületre.
Vajon milyen irányú és milyen nagyságú kell, hogy legyen ez a homogén erőtér? Az elrendezés szimmetriája miatt \(\displaystyle \boldsymbol p\)-vel párhuzamos (vagy azzal ellentétes irányú), a nagysága pedig éppen \(\displaystyle \vert {\boldsymbol E}_0\vert\), hiszen csak akkor teljesül, hogy a \(\displaystyle B\) pontban az eredő térerősségnek ne legyen érintőleges komponense. Ezek szerint
\(\displaystyle {\boldsymbol E}^\text{(összes)}={\boldsymbol E}^\text{(dipól)}+{\boldsymbol E}^\text{(homogén)}= {\boldsymbol E}^\text{(dipól)}-{\boldsymbol E}_B^\text{(dipól)}.\)
A kérdéses pontokban a térerősség nagysága:
\(\displaystyle E_A=2E_0-(-E_0)=3E_0=3p\cdot\frac{1}{4\pi\varepsilon_0 R^3},\)
illetve
\(\displaystyle E_B=-E_0-(-E_0)=0. \)
Ennek megfelelően a felületi töltéssűrűségek:
\(\displaystyle \sigma_A= -{\varepsilon}{E_A}=-3\frac{p}{4\pi R^3} \qquad \text{és} \qquad \sigma_B=0. \)
A gömbhéjon kívül az elektromos erőtér Coulomb-tér, aminek nagysága a gömbhéj belsejében lévő összes töltéssel arányos. Mivel ez a töltés nulla, kívül nincs elektromos erőtér, és így a felületi töltéssűrűség is nulla.
Megjegyzés. Megmutatjuk, hogy a dipól terének és a homogén elektromos térnek a szuperpoziciója valóban a fémfelületre merőleges vektorokat eredményez, nemcsak a Gauss-féle főhelyzetekben, hanem a dipól tengelyével tetszőleges \(\displaystyle \vartheta\) szöget bezáró helyvektorral jellemzett \(\displaystyle P\) pontban is.
A \(\displaystyle \boldsymbol p\) dipólmomentum vektor felbontható egy \(\displaystyle p\cos\varphi\) nagyságú \(\displaystyle \boldsymbol p_1\) és \(\displaystyle p\sin\varphi\) nagyságú \(\displaystyle \boldsymbol p_2\) vektor összegére (2. ábra). Ezen két dipólus szempontjából a \(\displaystyle P\) pont Gauss-féle (első, illetve második) főhelyzetnek számít, így a dipól terének komponensei:
\(\displaystyle E^\text{(dipól)}_\text{radiális}=2\cos\vartheta\,E_0,\)
\(\displaystyle E^\text{(dipól)}_\text{tangenciális}=-\sin\vartheta\,E_0,\)
ahol \(\displaystyle E_0\) az \(\displaystyle \frac{1}{4\pi\varepsilon_0}\frac{p}{R^3}\) mennyiséget jelöli.
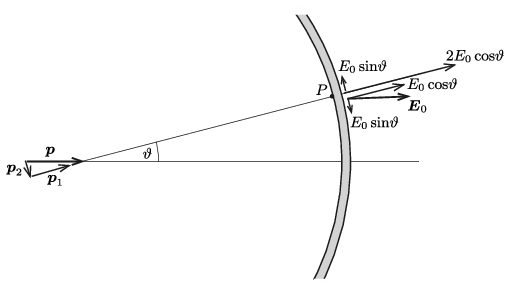
2. ábra
Szuperponáljuk a dipól terére az
\(\displaystyle \boldsymbol E_0=\frac{1}{4\pi\varepsilon_0 R^3}\boldsymbol p\)
térerősségvektorral megadott homogén elektromos mezőt. Ennek komponensei a gömbhéj belső felületénél:
\(\displaystyle E^\text{(homogén)}_\text{radiális}=\cos\vartheta\,E_0,\)
\(\displaystyle E^\text{(homogén)}_\text{tangenciális}=+\sin\vartheta\,E_0.\)
Az eredő térnek a gömbhéj felületénél a tangenciális komponense nulla, a radiális pedig:
\(\displaystyle E^\text{(eredő)}_\text{radiális}=3\cos\vartheta\,E_0=\frac{3p}{4\pi\varepsilon_0 R^3} \cos\vartheta.\)
Innen leolvasható, hogy a gömbhéj belső felületén a töltéssűrűség:
\(\displaystyle \sigma(\vartheta)=\frac{3p}{4\pi R^3}\cos\vartheta,\)
vagyis \(\displaystyle \vartheta=0\)-nál \(\displaystyle \sigma_A=\frac{3p}{4\pi R^3},\) valamint \(\displaystyle \vartheta=90^\circ\)-nál \(\displaystyle \sigma_B=0.\)
Statisztika:
7 dolgozat érkezett. 6 pontot kapott: Schmercz Blanka. 5 pontot kapott: Gábriel Tamás, Toronyi András. 4 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2022. februári fizika feladatai
