A P. 5409. feladat (2022. május)

P. 5409. Az ábrán egyszerű gépek kavalkádját láthatjuk. A súrlódás, valamint a csigák és emelők tömege elhanyagolható. Mekkora erő ébred a fonalakban?

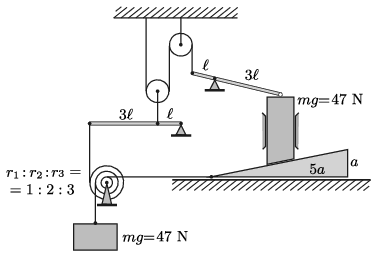
Holics László feladata nyomán

(4 pont)

A beküldési határidő 2022. június 15-én LEJÁRT.

Megoldás. A rendszer nyugalomban van (lásd a G. 784. gyakorlat megoldását), így valamennyi része külön-külön is egyensúlyban van.

Jelöljük a hengerkerék és az ék közötti fonalat feszítő erőt \(\displaystyle F\)-fel! Az ék által a felette lévő testre kifejtett erő függőleges komponense \(\displaystyle 5F\), az a test tehát \(\displaystyle 5F-mg\) erővel nyomja felfelé a kétoldalú emelő hosszabb karjának végét. (Jóllehet ez a nyomtatásban megjelent ábrán nem látszik, de feltételezzük, hogy az ék feletti test csak függőleges irányban tud elmozdulni.) Az emelő másik karja \(\displaystyle 3(5F-mg)\) erővel húzza lefelé az állócsigán átvetett fonalat. A mozgócsiga akkor van egyensúlyban, ha a tengelyéhez kapcsolódó fonalat \(\displaystyle 6(5F-mg)\) erő feszíti. Így az egykarú emelő végén lévő fonálban ébredő erő \(\displaystyle \tfrac32(5F-mg)\). A legalsó testet tartó fonalat feszítő erő nyilván \(\displaystyle mg\).

Egyensúlyban a hengerkerékre ható forgatónyomatékok előjeles összege nulla:

\(\displaystyle F\cdot r_1-2mg\cdot r_2+\frac32(5F-mg)\cdot r_3=0,\)

vagyis (a sugarak megadott arányának megfelelően)

\(\displaystyle F-2mg+\frac92(5F-mg)=0,\qquad \Rightarrow\qquad F=\frac{13}{47}\,mg=13~\rm N.\)

A csigákon átvetett fonalat \(\displaystyle 3(5F-mg)=54~\rm N\), a mozgócsiga tengelyéhez csatlakozó fonalat \(\displaystyle 6(5F-mg)=108~\rm N\), a hengerkerék legnagyobb tárcsájára tekert fonalat \(\displaystyle \tfrac32(5F-mg)=27~\rm N\) erő feszíti.

Megjegyzés. Ugyanerre az eredményre juthatunk úgy is, ha a hengerkerék és az egyoldalú emelő közötti fonálban ható erőt nevezzük el (mondjuk \(\displaystyle K\)-nak), és ezután vizsgáljuk végig a rendszer egyensúlyát lépésről lépésre, a fenti megoldáshoz képest ellenkező irányban.

Statisztika:

9 dolgozat érkezett.
4 pontot kapott:	Seprődi Barnabás Bendegúz, Toronyi András, Vig Zsófia.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2022. májusi fizika feladatai