A P. 5412. feladat (2022. május)

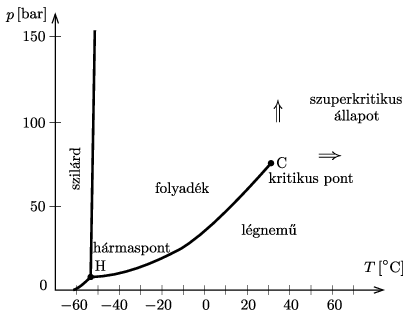
P. 5412. Ha egy gázt (állandó nyomás mellett) lehűtünk, akkor elegendően alacsony hőmérsékleten a gáz általában cseppfolyósodik (kondenzálódik, lecsapódik). Ez azonban csak bizonyos nyomástartományban történik így. Az ábra a szén-dioxid ,,fázisdiagramját'' mutatja. Legalább, illetve legfeljebb mekkora nyomás mellett történik meg a cseppfolyósodás a fenti módon? Mi történik, ha a hűtést ennél a tartománynál magasabb, illetve alacsonyabb nyomáson végezzük?

(Lásd még ,,A gőz, gáz és a kritikus hőmérséklet'' c. rövid cikket a KöMaL honlapján: https://www.komal.hu/cikkek/cikklista.h.shtml.)

Közli: Honyek Gyula, Veresegyház

(3 pont)

A beküldési határidő 2022. június 15-én LEJÁRT.

Megoldás. Az ábráról leolvashatjuk, hogy a gázt állandó nyomáson hűtve csak akkor cseppfolyósodik (folyadékcseppek képződésével és ezek fokozatos növekedésével), ha a nyomás a hármaspont \(\displaystyle p_{\rm H}\) nyomásánál nagyobb, de a kritikus pont \(\displaystyle p_{\rm C}\) nyomásnál kisebb.

A H hármaspont nyomásánál alacsonyabb nyomáson a lehűtött gáz közvetlenül (a folyadékállapot kihagyásával) szilárd halmazállapotúvá válik (inverz szublimáció, amit gőz depozíciónak, vagy röviden depozíciónak hívnak).

A kritikus pont nyomásánál nagyobb nyomásokon a légnemű anyag – a sűrűségének folyamatos (nem ugrásszerű) növekedése mellett – válik folyadékká. Ilyen körülmények között a gáz állapot (amit szuperkritikus állapotnak is neveznek) és a folyadékállapot ,,összemosódik'', nem különül el egymástól.

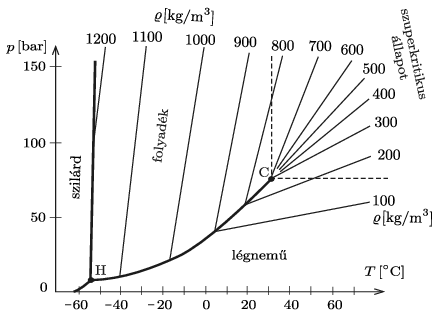
Jól látható ez az átmenet olyan ábrán, amelyen a sűrűséget is feltüntetik. A hármaspont és a kritikus pont között húzódó légnemű-folyadék fázishatáron (az ún. tenziógörbe mentén, amit forrási görbének is hívnak) a sűrűségnek ugrása van, a kritikus pontot ,,felülről'' megkerülve azonban az anyag sűrűsége folytonosan változik. A szuperkritikus állapot szaggatott vonalakkal jelölt határa nem igazi fizikai határvonal, nem ,,fázishatár'', hiszen azt átlépve semmi különleges nem történik, hanem csupán az önkényes szóhasználat határaira utal.

Statisztika:

9 dolgozat érkezett.
3 pontot kapott:	Horváth 221 Zsóka, Szabó Márton, Toronyi András.
2 pontot kapott:	Bogdán Benedek, Kovács Kinga, Veszprémi Rebeka Barbara, Waldhauser Miklós.
1 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2022. májusi fizika feladatai