 |
A P. 5453. feladat (2022. december) |
P. 5453. Az \(\displaystyle r = 0{,}2\) m sugarú, töltetlen fémgömb középpontjától \(\displaystyle d = 0{,}5\) m távolságra egy \(\displaystyle Q\) nagyságú ponttöltés helyezkedik el. Határozzuk meg (akár numerikus számítással), hogy a ponttöltéstől nézve mekkora szög alatt látszanak a fémgömb azon pontjai, ahol a felületi töltéssűrűség zérus!
Közli: Szász Krisztián, Budapest
(6 pont)
A beküldési határidő 2023. január 16-án LEJÁRT.
Megoldás. A felületi töltéssűrűség arányos a fémgömb felületénél kialakuló elektromos térerősség nagyságával, tehát a kérdés az, hogy ez a térerősség hol nulla.
A gömbön kívül kialakuló elektromos tér a gömbi tükörtöltés módszerével határozható meg. Az \(\displaystyle r\) sugarú gömb középpontjától \(\displaystyle d\) távolságban lévő \(\displaystyle Q\) töltés tükörtöltése egy, a gömb középpontjától \(\displaystyle \delta=kr\) távolságra elhelyezett \(\displaystyle -kQ\) töltés, ahol \(\displaystyle k=r/d<1\) állandó. A gömb felületén akkora lesz a térerősség, mint az ábrán látható módon elhelyezett \(\displaystyle Q\), \(\displaystyle -kQ\) és a gömb középpontjába helyezett \(\displaystyle +kQ\) töltés elektromos terének az eredője.
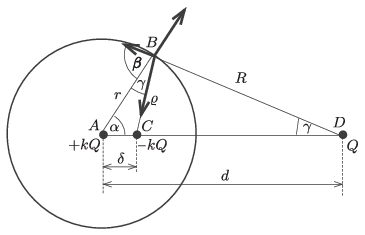
Az eredő térerősség mindenhol merőleges a gömb felületére, és a nagysága
| \(\displaystyle (1)\) | \(\displaystyle E=\frac{Q}{4\pi\varepsilon_0}\left(\frac{k}{r^2}-\frac{k\cos\gamma}{\varrho^2}-\frac{\cos\beta}{R^2}\right),\) |
ahol (a koszinusztétel szerint)
| \(\displaystyle (2)\) | \(\displaystyle \varrho=r\sqrt{1+k^2-2k\cos\alpha} \qquad \text{és}\qquad R=\frac{\varrho}{k}.\) |
(Kihasználtuk, hogy \(\displaystyle _\triangle ABC\) és \(\displaystyle _\triangle ADB\) hasonló háromszögek.)
Azt az \(\displaystyle \alpha\) szöget keressük, amelynél \(\displaystyle E=0\). A (2) összefüggéseket használva behelyettesíthetjük \(\displaystyle \varrho\)-t és \(\displaystyle R\)-t (1)-be, amely ezután így alakul:
| \(\displaystyle (3)\) | \(\displaystyle k\cos\beta+\cos\gamma=1+k^2-2k\cos\alpha.\) |
Két újabb koszinusztétel segítségével
| \(\displaystyle (4)\) | \(\displaystyle \cos\gamma=\frac{r^2+\varrho^2-\delta^2}{2r\varrho}=\frac{1-k\cos\alpha}{\sqrt{1+k^2-2k\cos\alpha}},\) |
illetve
\(\displaystyle \cos\beta=\frac{d^2-r^2-R^2}{2rR}=\frac{ \cos\alpha-k}{\sqrt{1+k^2-2k\cos\alpha}}.\)
Ezeket (3)-ba helyettesítve kapjuk, hogy
\(\displaystyle 1-k^2=\left(1+k^2-2k\cos\alpha\right)^{3/2},\)
vagyis
\(\displaystyle \cos\alpha=\frac {\left(1+k^2\right)-\left(1-k^2\right)^{2/3}} {2k}\)
adódik. Visszahelyettesítve (4)-be adódik a (tetszőleges \(\displaystyle k\)-ra érvényes) végeredmény:
\(\displaystyle \cos\gamma=\frac{(1-k^2)^{1/3}+(1-k^2)^{2/3}}{2}.\)
Esetünkben \(\displaystyle k=0{,}4\), ezért \(\displaystyle \cos\gamma=0{,}917\), azaz \(\displaystyle \gamma=23{,}51^\circ\). A kérdéses látószög tehát
\(\displaystyle 2\gamma=47{,}0^\circ.\)
Megjegyzés. Érdekes, hogy a kiszámított látószög nagyon jó közelítéssel megegyezik azzal a szöggel, amely alatt a teljes gömböt látjuk a \(\displaystyle Q\) töltés helyéről. Ez utóbbi
\(\displaystyle \gamma^*=\arcsin k=47{,}2^\circ.\)
Ez a közelítő egyezés nemcsak \(\displaystyle k=0{,}4\) esetén, hanem minden \(\displaystyle k\)-nál fennáll, tehát a zérus töltéssűrűségű hely majdnem a fémgömb látható részének legszélénél található. \(\displaystyle \gamma\) egy kicsit kisebb, mint \(\displaystyle \gamma^*\), de a relatív eltérésük tetszőleges \(\displaystyle k\) esetén kisebb, mint 2%.
Statisztika:
7 dolgozat érkezett. 6 pontot kapott: Bencz Benedek, Halász Henrik, Schmercz Blanka. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 2 versenyző.
A KöMaL 2022. decemberi fizika feladatai
