A P. 5488. feladat (2023. április)

P. 5488. $\displaystyle \alpha$-részecskéket $\displaystyle 10^6$ V feszültséggel felgyorsítunk, majd a nyalábot az ábrának megfelelően merőlegesen egy $\displaystyle B=1{,}5$ T indukciójú, $\displaystyle d=7$ cm szélességű, homogén mágneses mezőbe irányítjuk.

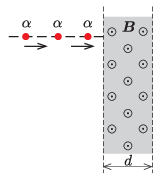
$\displaystyle a)$ Milyen szögben térülnek el a részecskék?

$\displaystyle b)$ Mennyi időt töltenek a részecskék a mágneses térben?

Közli: Holics László, Budapest

(4 pont)

A beküldési határidő 2023. május 15-én LEJÁRT.

Megoldás. A lényegében nyugvó helyzetből $\displaystyle U$ feszültséggel felgyorsított $\displaystyle \alpha$ részecskék sebességét az

$\displaystyle \frac{1}{2}m_{\alpha}v^2=q_{\alpha}U$

energiamérlegből számolva ($\displaystyle m_{\alpha}=6{,}6447\cdot10^{-27}\ \textrm{kg}$, $\displaystyle q_{\alpha}=2e=3{,}20435\cdot10^{-19}\ \textrm{C}$, azaz $\displaystyle (q/m)_{\alpha}=4{,}8224\cdot10^7\ \textrm{C/kg}$ mellett)

$\displaystyle v=9{,}82\cdot 10^{6}\ \textrm{m/s}$

adódik. (Ez a fénysebesség $\displaystyle \beta=3{,}274\cdot 10^{-2}$-szöröse, így $\displaystyle {\beta}^2=1{,}072\cdot 10^{-3}$, azaz adataink pontossága mellett biztos használhatjuk a klasszikus közelítést.)

A mágneses térben az $\displaystyle \alpha$ részecskék a Lorentz erő (mint centripetális erő) hatására körpályán haladnak. Ennek sugara az

$\displaystyle \frac{m_{\alpha}v^2}{R}=q_{\alpha}vB$

összefüggésből

$\displaystyle R=\frac{v}{B\left(q/m\right)_{\alpha}}=0{,}136\ \textrm{m}.$

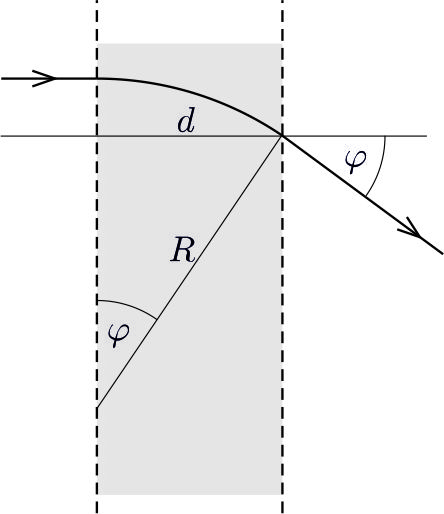
$\displaystyle a)$ Az eltérítés szöge az ábra szerint

$\displaystyle \varphi=\arcsin(d/R)=0{,}541\ \textrm{rad}=31{,}0^\circ .$

$\displaystyle b)$ A $\displaystyle \varphi$ nyílásszöghöz tartozó $\displaystyle R\varphi$ körív befutásához az $\displaystyle v$ sebességgel haladó részecskéknek

$\displaystyle t=\frac{R\varphi}{v}=7{,}49\cdot10^{-9}\ \textrm{s}$

időre van szükségük, azaz ennyit töltenek a mágneses térben.

Statisztika:

34 dolgozat érkezett.
4 pontot kapott:	Beke Bálint, Benes András, Bocor Gergely, Chrobák Gergő, Éger Viktória, Fórizs Borbála, Gerendás Roland, Halász Henrik, Katona Attila Zoltán, Klement Tamás, Lévai Dominik Márk, Molnár Kristóf, Nemeskéri Dániel, Schmercz Blanka, Seprődi Barnabás Bendegúz, Szabó Zsombor, Szécsényi-Nagy Rudolf, Waldhauser Miklós.
3 pontot kapott:	Bodré Zalán, Bogdán Benedek, Vásárhelyi István Péter.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2023. áprilisi fizika feladatai