Problem P. 5580. (September 2024)

P. 5580. Two siblings, Anne and Brian are ``fighting'' with sock balls in the stairwell of their house, from a distance of \(\displaystyle 4.5~\mathrm{m}\) (measured horizontally) as shown in the figure. Anne throws the sock ball from the landing at a height of \(\displaystyle 4~\mathrm{m}\) with an initial horizontal velocity of \(\displaystyle 6~\mathrm{m}/\mathrm{s}\) and Brian throws the sock ball from a height of \(\displaystyle 1.5~\mathrm{m}\) with an initial velocity of \(\displaystyle 8~\mathrm{m}/\mathrm{s}\), making an angle of \(\displaystyle 45^\circ\) with the horizontal. Find the minimum distance between the two sock balls if the children threw them at the same time. (Neglect air resistance.)

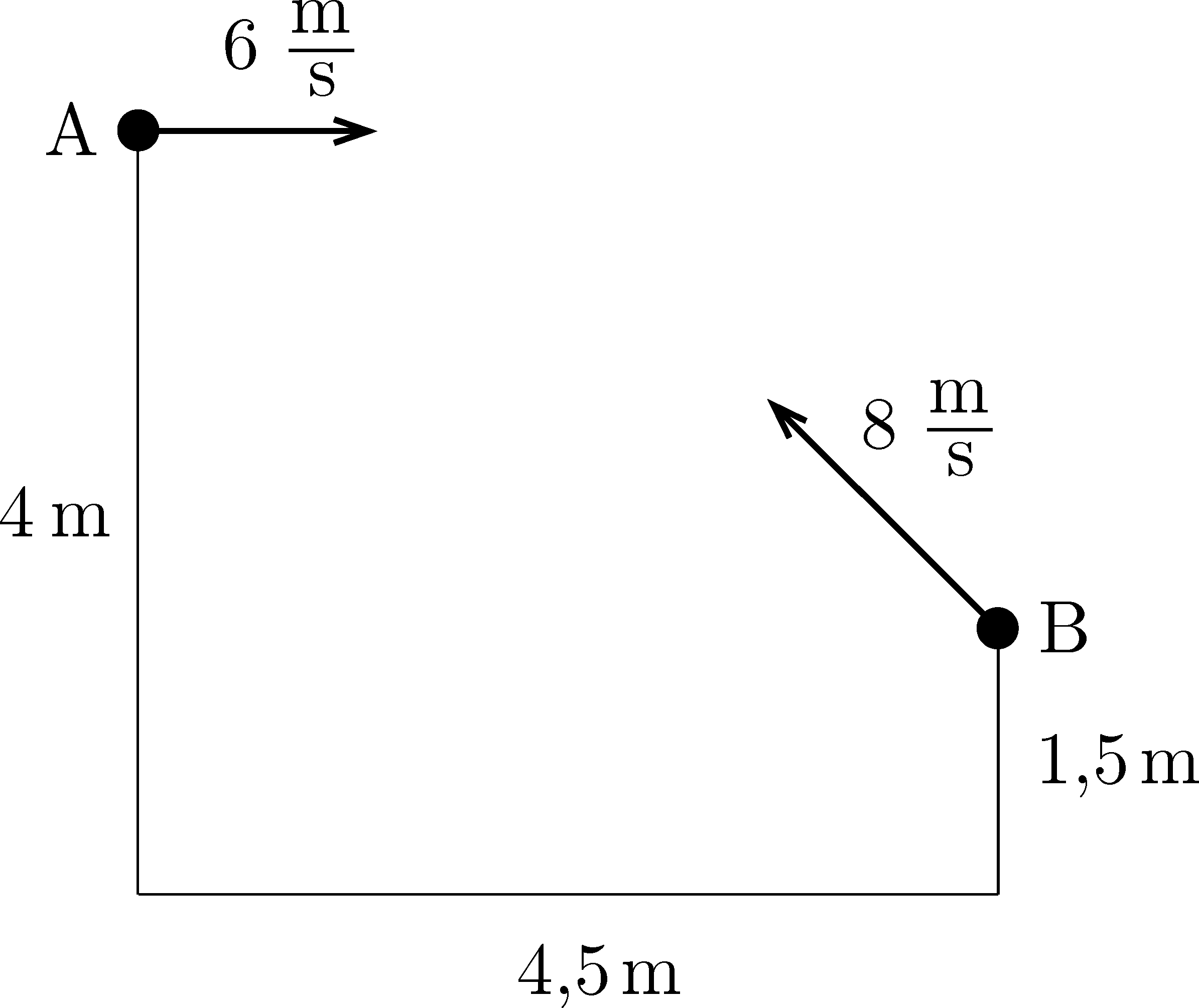
(4 pont)

Deadline expired on October 15, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Vizsgáljuk a két test mozgását az \(\displaystyle A\) pontból eldobott testtel együtt mozgó (vízszintesen \(\displaystyle v_A=6\,\mathrm{m/s}\) sebességgel egyenletesen mozgó, függőlegesen lefelé \(\displaystyle g\) gyorsulással gyorsuló) koordináta-rendszerből. Ebben a rendszerben a \(\displaystyle B\) pontból \(\displaystyle v_B=8\,\mathrm{m/s}\) sebességgel eldobott test \(\displaystyle \boldsymbol{v}_\mathrm{rel}=\boldsymbol{v}_B-\boldsymbol{v}_A\) sebességgel egyenes vonalú egyenletes mozgást végez, sebességének iránya a vízszintessel

\(\displaystyle \alpha=\arctg\frac{v_B\sin 45^\circ}{v_A+v_B\cos 45^\circ}=\arctg\frac{4\sqrt{2}}{6+4\sqrt{2}}=25{,}9^\circ\)

szöget zár be. (Az \(\displaystyle A\) pont pedig értelemszerűen nyugalomban van.)

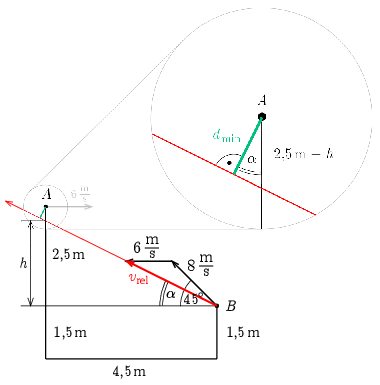
Az ábra alapján \(\displaystyle h=4{,}5\,\mathrm{m}\cdot\tg\alpha=2{,}18\,\mathrm{m}\), a két eldobott test közötti minimális távolság pedig a kinagyított ábrarészlet alapján \(\displaystyle d_\mathrm{min}=(2{,}5\,\mathrm{m}-h)\cos\alpha=0{,}28\,\mathrm{m}=28\,\mathrm{cm}\).

Statistics:

75 students sent a solution.
4 points:	Agócs Zoltán, Bálint Áron, Beke Márton Csaba, Bélteki Teó, Bencze Mátyás, Bense Tamás, Blaskovics Ádám, Bús László Teodor, Csapó András, Csiszár András, Domján Noémi Dóra, Elekes Panni, Éliás Kristóf , Erdélyi Dominik, Erős Fanni, Fekete Lúcia, Földi Albert, Gyenes Károly, Hajós Boróka, Hornok Máté, Horvath Benedek, Kiss 131 Adorján Timon, Klement Tamás, Kovács Dániel, Kovács Tamás, Magyar Zsófia, Masa Barnabás, Misik Balázs, Molnár Lili, Papp Emese Petra, Simon János Dániel, Szabó Márton, Tóth Hanga Katalin, Tóth-Tűri Bence, Ujvári Sarolta, Varga 511 Vivien, Vértesi Janka, Vincze Anna, Zólomy Csanád Zsolt.
3 points:	Beinschroth Máté, Kis Boglárka 08, Nagy Gellért Ákos, Orbán Jázmin, Sütő Áron, Szécsi Bence, Zádori Gellért, Zámbó Luca.
2 points:	4 students.
1 point:	4 students.
0 point:	11 students.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Physics of KöMaL, September 2024