 |
A P. 5592. feladat (2024. október) |
P. 5592. Egy elhanyagolható tömegű, nyújthatatlan kötél felfüggesztési pontjai az ábrán látható módon egymástól \(\displaystyle L\) vízszintes és \(\displaystyle H\) függőleges távolságra helyezkednek el. Egy hideg téli napon a \(\displaystyle \varrho\) sűrűségű hó \(\displaystyle d\) szélességben halmozódott fel a kötélen. A hóréteg magassága pedig zérus, illetve \(\displaystyle h_\textrm{max}\) értékek között lineárisan változik a vízszintes koordináta függvényében. A kialakult egyensúlyi helyzetben a kötél érintője jobb oldali végpontjánál éppen vízszintes. Határozzuk meg a kötélben ébredő legkisebb és legnagyobb húzóerőt!
Dürer Verseny feladata nyomán
(5 pont)
A beküldési határidő 2024. november 15-én LEJÁRT.
Megoldás. A megoldás első lépéseként gondoljuk végig, hogy a kötél mely keresztmetszetében lép fel a minimális, illetve maximális húzóerő! Tudjuk, hogy erő csak a kötél irányában ébredhet, ebből következik, hogy a jobb oldali végpontban fellépő húzóerő éppen vízszintes. Mivel a felhalmozódott hó tömegéből származó erőhatás függőleges irányú, és más külső erő nem hat a rendszerre, a kötélben keletkező húzóerő vízszintes komponense minden keresztmetszetben megegyezik. Az előzőekből egyértelműen következik, hogy a minimális kötélerő éppen a jobb oldali végpontban lép fel, míg a maximális érték a bal oldali végpontban keletkezik (hiszen a kötél érintőjének meredeksége, és így a függőleges irányú erőkomponens itt a legnagyobb).
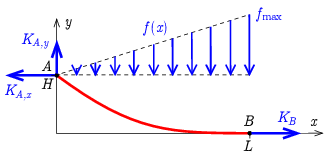
A fentiek alapján rajzoljuk fel a kötélre ható erőket, ezt szemlélteti az ábra. Jelölje a kötél bal oldali végpontját \(\displaystyle A\), jobb oldali végpontját pedig \(\displaystyle B\)! Ekkor az \(\displaystyle A\) pontban fellépő húzóerő komponensei legyenek \(\displaystyle K_{A,y}\) és \(\displaystyle K_{A,x}\), a \(\displaystyle B\) pontban keletkező húzóerőt pedig jelölje \(\displaystyle K_B\). A felhalmozódott hó hatását egy, a kötél vízszintes vetülete mentén lineárisan változó erőként kezelhetjük, melynek \(\displaystyle f=\tfrac{\Delta F}{\Delta x}\) ,,intenzitása'' a kötél bal oldali végpontján zérus, jobb oldalán pedig
\(\displaystyle f_\mathrm{max}=\varrho gdh_\mathrm{max}.\)
A továbbiakban vizsgáljuk a kötél, mint kiterjedt test egyensúlyát! Ekkor tudjuk, hogy a kötélre ható erők, valamint forgatónyomatékok eredőjének bármely pontra nézve zérusnak kell lennie. Felírva vízszintes irányban az erők eredőjére vonatkozó feltételt:
\(\displaystyle K_{A,x}=K_B,\)
továbbá függőleges irányban:
\(\displaystyle K_{A,y}=\frac{f_\mathrm{max}L}{2}=\frac{\varrho gdh_\mathrm{max}L}{2}.\)
Írjuk fel a testre ható forgatónyomatékokat az \(\displaystyle A\) pontra:
\(\displaystyle K_BH=\frac{f_\mathrm{max}L}{2}\cdot\frac{2}{3}L=\frac{f_\mathrm{max}L^2}{3},\)
beírva \(\displaystyle f_\mathrm{max}\) kifejezését, majd \(\displaystyle K_B\)-re rendezve:
\(\displaystyle K_B=\frac{\varrho gdh_\mathrm{max}L^2}{3H}.\)
Azaz a kötélben keletkező minimális húzóerő:
\(\displaystyle K_\mathrm{min}=K_B=\frac{\varrho gdh_\mathrm{max}L^2}{3H},\)
a fellépő maximális erő pedig a Pitagorasz-tételt felhasználva:
\(\displaystyle K_\mathrm{max}=\sqrt{K^2_{A,x}+K^2_{A,y}}=\frac{\varrho gdh_\mathrm{max}L}{6H}\sqrt{9H^2+4L^2}.\)
Statisztika:
A P. 5592. feladat értékelése még nem fejeződött be.
A KöMaL 2024. októberi fizika feladatai