A P. 5593. feladat (2024. október)

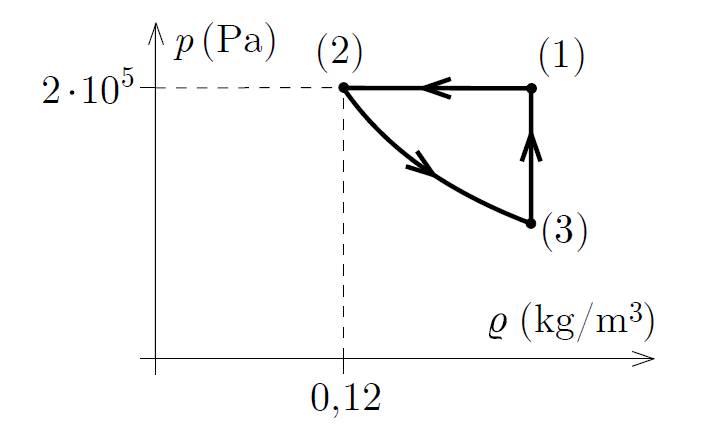
P. 5593. Állandó mennyiségű héliumgázzal üzemelő hőerőgép körfolyamatának részleteit követhetjük nyomon a mellékelt nyomás-sűrűség diagramon. A gáz hőmérséklete a kiinduló, $\displaystyle (1)$-es állapotában $\displaystyle 400~\mathrm{K}$, a $\displaystyle (2)$-es és a $\displaystyle (3)$-as állapotai között végbemenő folyamatban pedig nyomásának és sűrűségének szorzata állandó.

$\displaystyle a)$ Mekkora a gáz hőmérséklete a $\displaystyle (2)$-es és a $\displaystyle (3)$-as állapotban?

$\displaystyle b)$ Mekkora ennek a hőerőgépnek a hatásfoka?

Tornyai Sándor fizikaverseny, Hódmezővásárhely

(5 pont)

A beküldési határidő 2024. november 15-én LEJÁRT.

Megoldás. a) Az ideális gáz állapotegyenlete:

$\displaystyle pV=\frac{mRT}{M}\quad\rightarrow\quad p=\frac{\varrho RT}{M},$

ahol $\displaystyle R=8{,}314\,\mathrm{\tfrac{J}{mol\,K}}$, $\displaystyle M=0{,}004\,\mathrm{\tfrac{kg}{mol}}$, és így $\displaystyle \tfrac{M}{R}=0{,}000481\,\mathrm{\tfrac{kg\,K}{J}}$. Ebből

$$\begin{align*} \varrho_1&=\frac{p_1}{T_1}\cdot\frac{M}{R}\approx 0{,}24\,\mathrm{\frac{kg}{m^3}}\\ T_2&=\frac{p_2}{\varrho_2}\cdot\frac{M}{R}\approx 800\,\mathrm{K}. \end{align*}$$

A (3)$\displaystyle \rightarrow$(1) folyamatban a sűrűség állandó, így

$\displaystyle \varrho_3=\varrho_1\approx 0{,}24\,\mathrm{\frac{kg}{m^3}}.$

A (2)$\displaystyle \rightarrow$(3) folyamatban $\displaystyle p\varrho=\textrm{állandó}$, így

$\displaystyle p_3=\frac{p_2\varrho_2}{\varrho_3}\approx 100\,\mathrm{kPa}.$

Ezekből, ismét az állapotegyenletet használva

$\displaystyle T_3=\frac{p_3}{\varrho_3}\cdot\frac{M}{R}\approx 200\,\mathrm{K}.$

A gáz állapotjelzőit a folyamat megjelölt pontjain az 1. táblázatban foglaltuk össze.

1. táblázat

b) Rajzoljuk át a folyamatot a $\displaystyle p\,$-$\displaystyle V$ állapotsíkra (ábra)!

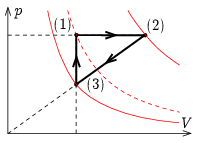
Az (1)$\displaystyle \rightarrow$(2) folyamatban a nyomás állandó, a sűrűség csökken, így a térfogat nő, tehát ez egy izobár tágulás. A (2)$\displaystyle \rightarrow$(3) folyamatban a $\displaystyle p\varrho$ szorzat állandóságából következően a $\displaystyle \tfrac{p}{V}$ hányados állandó, azaz a folyamat a $\displaystyle p\,$-$\displaystyle V$ állapotsíkon egy origón átmenő egyenesre illeszkedő szakasz. Végül a (3)$\displaystyle \rightarrow$(1) folyamatban a sűrűség állandóságából következtetően a térfogat is állandó, ez egy izochor folyamat.

Az ábrára berajzoltuk a (3)-as és (2)-es állapoton (folytonos piros vonallal), valamint a köztes, (1)-es állapoton (szaggatott piros vonallal) áthaladó adiabatákat. Láthatjuk, hogy a gáz a (3)$\displaystyle \rightarrow$(1) és (1)$\displaystyle \rightarrow$(2) folyamatban hőt vesz fel, a (2)$\displaystyle \rightarrow$(3) folyamatban pedig hőt ad le.

A (3)$\displaystyle \rightarrow$(1) izochor folyamatban a hőfelvétel

$\displaystyle Q_{\textrm{fel},3\rightarrow 1}=\frac{3}{2}nR(T_1-T_3)=300\,\mathrm{K}\cdot nR,$

az (1)$\displaystyle \rightarrow$(2) izobár folyamatban a hőfelvétel

$\displaystyle Q_{\textrm{fel},1\rightarrow 2}=\frac{5}{2}nR(T_2-T_1)=1000\,\mathrm{K}\cdot nR.$

A teljes körfolyamat alatt a gáz munkavégzése a $\displaystyle p\,$-$\displaystyle V$ állapotsíkon a körfolyamat által körbezárt terület nagysága:

$\displaystyle W_\mathrm{g}=\frac{1}{2}(p_1-p_3)(V_2-V_1)=\frac{nR}{2}(p_1-p_3)\left(\frac{T_2}{p_2}-\frac{T_1}{p_1}\right)=100\,\mathrm{K}\cdot nR.$

Ez alapján a hőerőgép hatásfoka

$\displaystyle \eta=\frac{W_\mathrm{g}}{Q_\mathrm{fel}}=\frac{100\,\mathrm{K}\cdot nR}{1300\,\mathrm{K}\cdot nR}=\frac{1}{13}\approx 7{,}7\%.$

A folyamatok jellemzőit a 2. táblázatban foglaltuk össze.

2. táblázat

Megjegyzés. A hatásfokot azért nem lehet a Carnot-folyamatból ismert $\displaystyle \eta=\tfrac{T_\mathrm{max}-T_\mathrm{min}}{T_\mathrm{max}}$ összefüggéssel számolni, mert ez nem egy Carnot-körfolyamat, esetünkben a hőfelvétel közben a gáz hőmérséklete – a Carnot-folyamattal ellentétben – folyamatosan változik, és így a hőcseréhez (elvileg) végtelen sok hőtartályra lenne szükség, hiszen reverzibilis hőátadás csak (majdnem) azonos hőmérsékletű hőtartályok között lehetséges. Ha a hőfelvétel végig egy $\displaystyle T_\mathrm{max}=800\,\mathrm{K}$-es ,,felső'' és egy $\displaystyle T_\mathrm{min}=200\,\mathrm{K}$-es ,,alsó'' hőtartályhoz kapcsolva történik, akkor a hőátadás irreverzibilis lesz, és így az entrópia nem marad állandó (növekszik), a hatásfok pedig rosszabb lesz, mint az ekkora hőmérsékletek között működő Carnot-gépé.

A gyakorlatban a sok hőtartály helyett például ellenáramlásos hőátadást használnak: a hideg gázt kezdetben a felmelegedett hűtőközeg melegíti (ahogyan a modern kéményekben a beáramló hideg levegőt a kiáramló forró égéstermék), és ezzel a hatásfok javítható. Természetesen az elvi határt jelentő Carnot-hatásfokot nem lehet túllépni.

Statisztika:

A P. 5593. feladat értékelése még nem fejeződött be.

A KöMaL 2024. októberi fizika feladatai

Már regisztráltál?
Új vendég vagy?