A P. 5594. feladat (2024. október)

P. 5594. Nagy területű síkkondenzátor lemezei között, azokkal párhuzamosan egy-egy kör alakú, $\displaystyle R$ sugarú, töltetlen fémkorong található, melyeket több vékony, nyújtatlan fémszál köt össze. A felső korongot vékony szigetelő pálcák rögzített helyzetben tartják. Mindkét korong $\displaystyle d\ll R$ távolságban van a hozzá közelebbi lemeztől (lásd az ábrát).

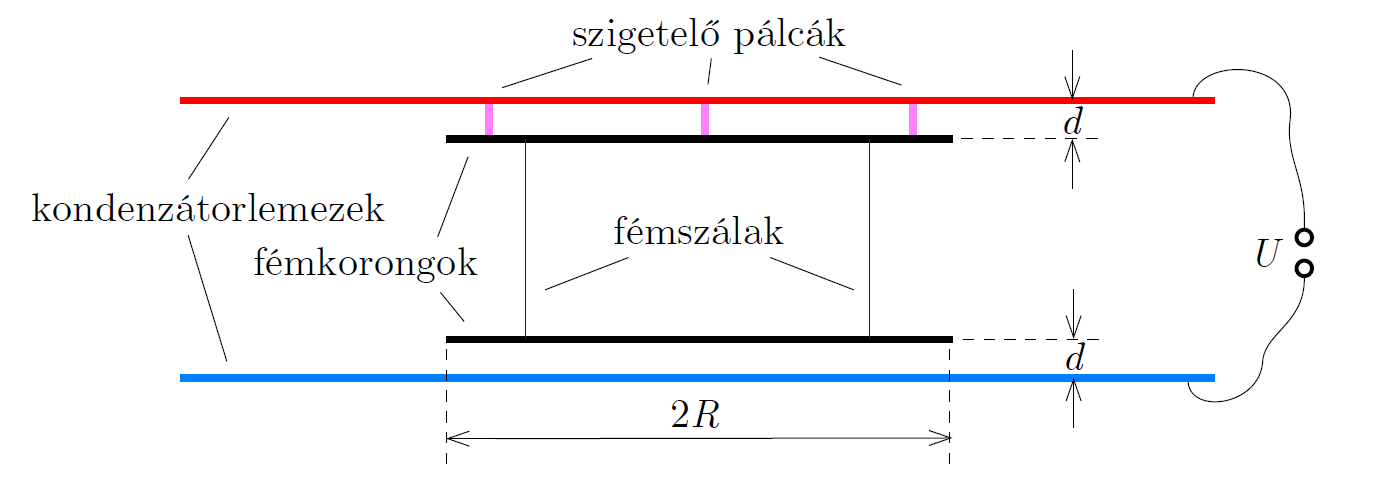
Mennyivel változik a fémszálak együttes húzóereje, ha a kondenzátorra $\displaystyle U$ feszültséget kapcsolunk?

Adatok: $\displaystyle R=10~\mathrm{cm}$, $\displaystyle d=0{,}5~\mathrm{cm}$, $\displaystyle U=5000~\mathrm{V}$.

Közli: Gnädig Péter, Vácduka

(5 pont)

A beküldési határidő 2024. november 15-én LEJÁRT.

Megoldás. A fémkorongok ekvipotenciálisak, hiszen azokat elektromosan vezető fémszálak kötik össze. Emiatt a fémkorongok közötti térrészben az elektromos térerősség nullának tekinthető (legfeljebb a korongok szélénél alakulhat ki ,,szórt'' elektromos mező).

A kondenzátor $\displaystyle U$ feszültsége a fémkorongok és a kondenzátorlemezek közötti, összesen $\displaystyle 2d$ szélességű sávokból származik, vagyis a lemezekre merőleges irányú elektromos térerősség nagysága

$\displaystyle E=\frac{U}{2d}.$

Az alsó fémkorong alsó felületén – az elektromos megosztás következtében felületegységenként $\displaystyle \sigma=\varepsilon_0E$ töltés halmozódik fel, amire az $\displaystyle E$ nagyságú elektromos tér felületegységenként

$\displaystyle p=\frac{1}{2}\sigma E=\frac{\varepsilon_0 E^2}{2}=\frac{\varepsilon_0U^2}{8d^2}$

erőt fejt ki.

Az alsó fémkorongra ható teljes elektrosztatikus erő

$\displaystyle F=p\cdot R^2\pi=\frac{\varepsilon_0U^2R^2\pi}{8d^2}=0{,}035\,\mathrm{N}.$

Ennyivel nő meg a fémszálak együttes húzóereje a kondenzátor feltöltésének hatására.

Statisztika:

10 dolgozat érkezett.
5 pontot kapott:	Beke Márton Csaba, Erdélyi Dominik, Ujpál Bálint, Zólomy Csanád Zsolt.
4 pontot kapott:	Fekete Lúcia, Sütő Áron, Tóth Kolos Barnabás.
3 pontot kapott:	1 versenyző.

A KöMaL 2024. októberi fizika feladatai