A P. 5595. feladat (2024. október)

P. 5595. Két, kis nyílásszögű, $\displaystyle f$ fókusztávolságú homorú tükröt tükröző felületeikkel szemben úgy helyezünk el, hogy optikai tengelyeik egybeessenek, és egymástól való távolságuk $\displaystyle 2f$ legyen (lásd ábra).

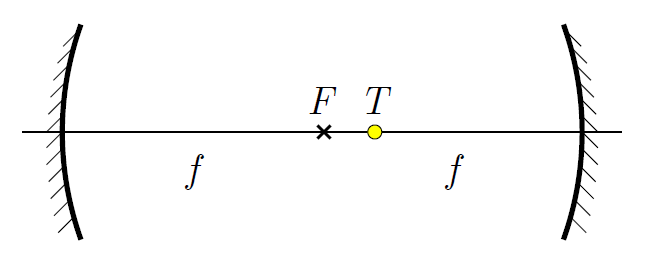
A közös optikai tengelyre hová helyezzük a $\displaystyle T$, pontszerűnek tekinthető fényforrást, hogy a belőle induló fénysugarak a két tükörről való visszaverődés után a $\displaystyle T$ ponton menjenek át?

Közli: Zsigri Ferenc, Budapest

(4 pont)

A beküldési határidő 2024. november 15-én LEJÁRT.

I. megoldás. Az első leképzésnél a tárgytávolság (a $\displaystyle T$ pont és az egyik tükör távolsága) legyen $\displaystyle t_1$. Ekkor az első tükröződés után keletkező kép $\displaystyle k_1$ távolsága a leképzési törvény $\displaystyle \left(\tfrac{1}{f}=\tfrac{1}{t}+\tfrac{1}{k}\right)$ alapján:

$\displaystyle k_1=\frac{ft_1}{t_1-f}.$

Az első kép távolsága a másik tükörtől ($\displaystyle t_2$):

$\displaystyle t_2=2f-k_1=\frac{f(t_1-2f)}{t_1-f},$

és ebből a $\displaystyle k_2$ második képtávolság:

$\displaystyle k_2=\frac{ft_2}{t_2-f}=2f-t_1.$

Azaz a második leképzés után a kép a $\displaystyle t_1$ távolságtól függetlenül a $\displaystyle T$ pontra esik, a fényforrás tehát bárhol lehet.

Megjegyzés. Ha $\displaystyle t_1>f$, akkor az első kép valódi lenne, de a másik tükör mögé esik, így a második leképzésnek egy virtuális tárgya van (1. ábra). Ha $\displaystyle t_1<f$, akkor az első leképzésnél látszólagos kép keletkezik, ezt képezi le a második visszaverődés (2. ábra). A második leképzés után viszont mindenképp valódi képet kapunk, és a végső nagyítás minden esetben $\displaystyle N=N_1N_2=\tfrac{k_1}{t_1}\,\tfrac{k_2}{t_2}=-1$ lesz, tehát a kép mérete megegyezik a tárgyéval, de fordított állású lesz.

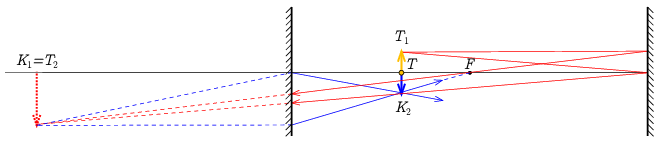
1. ábra

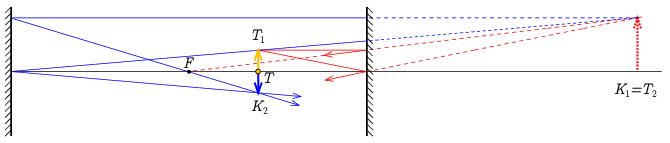
2. ábra

$\displaystyle t_1=f$ esetében nem keletkezik az első tükröződés után kép, a fókuszsíkból induló fénysugarak a tükörről párhuzamosan verődnek vissza, amelyeket a másik tükör ismét a fókuszsíkba gyűjt, tehát ilyenkor is teljesül, hogy a fénysugarak kétszeres visszaverődés után a $\displaystyle T$ ponton mennek át (3. ábra).

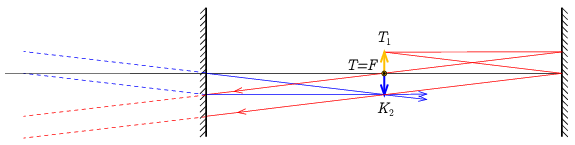
3. ábra

(Az ábrákon a fény először a jobb oldali, aztán a bal oldali tükrön tükröződik, de ennek az elrendezés szimmetriája miatt nincs jelentősége.)

II. megoldás. Még egyszerűbben jutunk az eredményre, ha a leképzési törvény Newton-féle alakját használjuk (lásd a G. 855. gyakorlatot a 2024.  évi májusi számában és a megoldását a munkafüzetben). Ekkor a ,,fókuszontúli'' tárgy- és képtávolság $\displaystyle x_\mathrm{t}=t-f$, illetve $\displaystyle x_\mathrm{k}=k-f$, és ezekre teljesül az $\displaystyle x_\mathrm{t}x_\mathrm{k}=f^2$ összefüggés. Esetünkben ez azt jelenti, hogy az $\displaystyle x_\mathrm{t}$ és $\displaystyle x_\mathrm{k}$ távolságokat a közös fókuszponttól kell mérni, és így $\displaystyle x_\mathrm{t2}=-x_\mathrm{k1}$, amiből azonnal $\displaystyle x_\mathrm{k2}=-x_\mathrm{t1}$ következik bármely $\displaystyle x_\mathrm{t1}$ esetében.

Statisztika:

29 dolgozat érkezett.
4 pontot kapott:	Blaskovics Ádám.
3 pontot kapott:	Bense Tamás, Bús László Teodor, Csiszár András, Kis Boglárka 08, Tóth-Tűri Bence, Vincze Anna.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	2 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2024. októberi fizika feladatai