 |
A P. 5618. feladat (2025. január) |
P. 5618. Egy \(\displaystyle m\) tömegű gyöngyöt fűztünk egy elegendően hosszú, függőleges helyzetű, rögzített, feszes drótra, amelyhez egy fonalat erősítettünk. A fonalat, az ábra szerint egy vízszintes rúdon átvetettünk, és függőleges darabjának végéhez egy kicsiny, \(\displaystyle 2m\) tömegű nehezéket rögzítettünk. A rúd a dróttól \(\displaystyle d\) távolságra van. A gyöngyhöz kapcsolódó fonalszál vízszintes helyzetében a gyöngynek felfelé mutató, \(\displaystyle v_0=\sqrt{2gd}\) nagyságú kezdősebességet adunk.
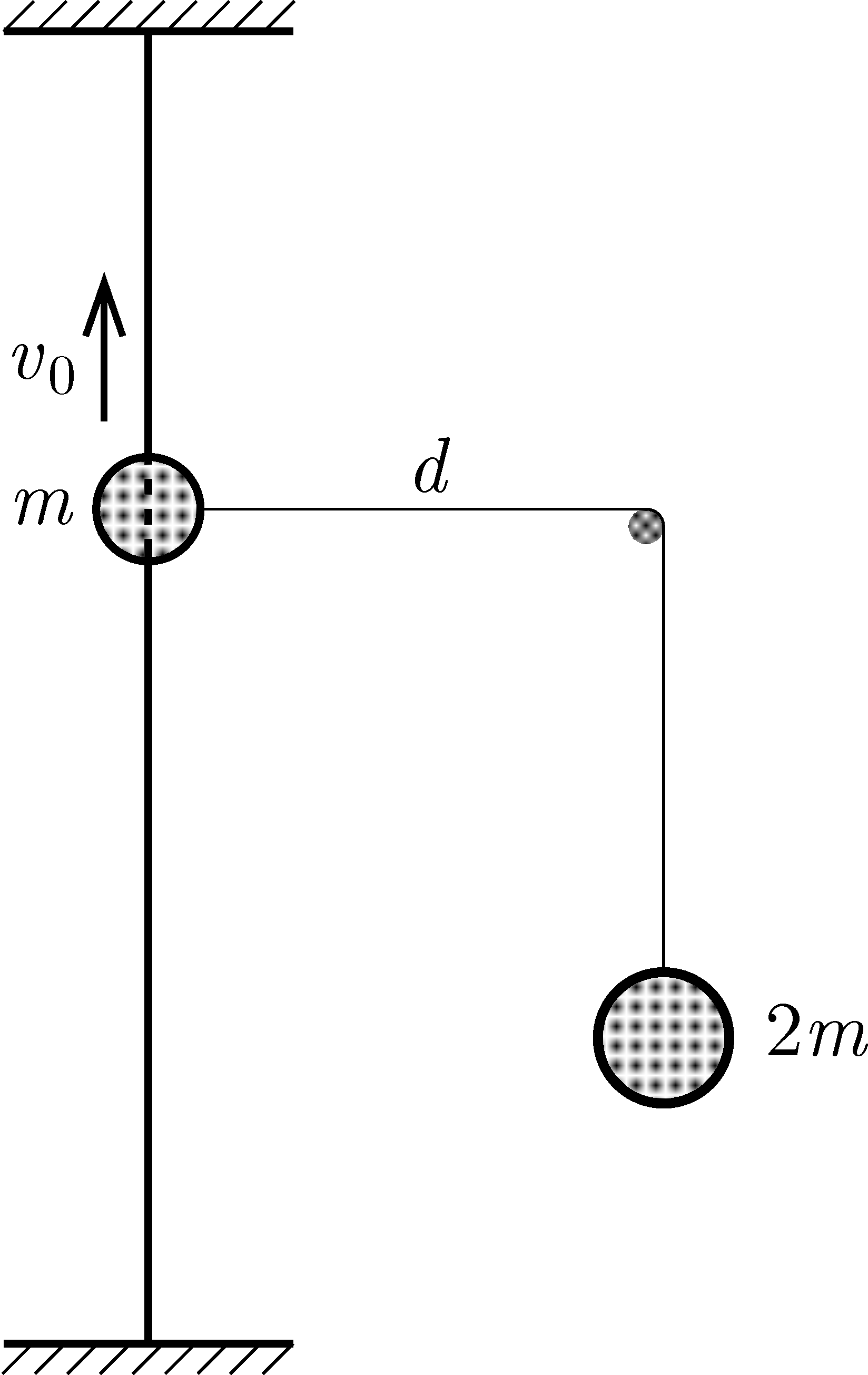
a) A gyöngy legfelső helyzetének a kiindulási ponttól való távolsága legyen \(\displaystyle f\), a legalsó helyzetének a kiindulási ponttól való távolsága pedig \(\displaystyle \ell\). Mekkora az \(\displaystyle \ell/f\) hányados?
b) Mekkora a fonálban ébredő erő a gyöngy legfelső helyzetében és a kiindulási ponton való áthaladáskor?
(A súrlódás mindenhol elhanyagolható.)
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2025. február 17-én LEJÁRT.
Megoldás. Az a pályapont, amikor a fonálnak a gyöngyhöz rögzített szakasza vízszintes, nem egyensúlyi helyzet, de kitünteti, hogy a fonálon lógó test ilyenkor van a legmélyebben, és a sebessége ebben a helyzetben mindig nulla.
a) A szélső helyzetek pozícióit legegyszerűbben az energiamegmaradás törvényének segítségével számolhatjuk ki. A fentiek alapján a kiinduló helyzetben csak a gyöngy mozog, a kinetikus energiája pedig a feladatban megadott kezdősebességet behelyettesítve:
\(\displaystyle \frac{1}{2}mv_0^2=mgd.\)
Mérjük az elmozdulásokat a kiindulási helyzettől, ezek legyenek pozitívak, ha fölfelé mutatnak, és jelöljük a gyöngy és a lógó test magasságát a szélső helyzetben \(\displaystyle h_1\) illetve \(\displaystyle h_2\)-vel. Az energiamérleg szerint
\(\displaystyle mgd=mgh_1+2mgh_2.\)
A két magasság között a kötél nyújthatatlanságát kifejező egyenlet ad összefüggést. Ha a gyöngy pozíciója \(\displaystyle x_1\), a fonálon függő testé pedig \(\displaystyle x_2\), a Pitagorasz tétel szerint
\(\displaystyle x_1^2+d^2=\left(d+x_2\right)^2,\)
a szélső helyzetben tehát
\(\displaystyle \sqrt{h_1^2+d^2}-d=h_2.\)
Egyszerűsítések és a \(\displaystyle h_2\) kiküszöbölése a
\(\displaystyle 3d=h_1+2\sqrt{h_1^2+d^2}\)
egyenletre vezet, amelyből átrendezéssel és négyzetre emeléssel a
\(\displaystyle 3h_1^2+6dh_1-5d^2=0\)
másodfokú egyenlet kapható. Ennek a pozitív gyöke éppen \(\displaystyle f\), a negatív gyöke pedig az \(\displaystyle l\) mínusz egyszerese:
$$\begin{gather*} f=\left(\sqrt{\frac{8}{3}}-1\right)d,\\ l=\left(\sqrt{\frac{8}{3}}+1\right)d, \end{gather*}$$tehát
\(\displaystyle \frac{l}{f}=\frac{\sqrt{8}+\sqrt{3}}{\sqrt{8}-\sqrt{3}}=4{,}16.\)
b) A kötélerő meghatározásához a mozgásegyenleteket kell felírnunk! Jelöljük a gyöngy és a fonálon függő test gyorsulását \(\displaystyle a_1\) és \(\displaystyle a_2\)-vel, legyen \(\displaystyle K_1\) a fonalban ható erő, és \(\displaystyle \varphi\) a gyöngyhöz csatlakozó fonaldarab vízszintessel bezárt szöge a szélső helyzetben (\(\displaystyle \sin\varphi=f/\sqrt{f^2+d^2}\))! Ezekkel
$$\begin{gather*} ma_1=-mg-K_1\sin\varphi,\\ 2ma_2=-2mg+K_1. \end{gather*}$$A szélső helyzet közelében az egyes testek pozíciói (hiszen itt a sebesség zérus)
\(\displaystyle x_1=f+\frac{1}{2}a_1(\Delta t)^2,\)
illetve
\(\displaystyle x_2=h_2+\frac{1}{2}a_2(\Delta t)^2\)
alakúak, (ahol a gyorsulások értéke negatív, és a \(\displaystyle \Delta t\) az az idő, ami a szélső helyzet eléréséhez kell, vagy azóta eltelt). Ezeket az értékeket helyettesítve a kényszeregyenletbe, az összefüggést ad a két gyorsulás között:
\(\displaystyle \left(f+\frac{1}{2}a_1(\Delta t)^2\right)^2+d^2=\left(d+h_2+\frac{1}{2}a_2(\Delta t)^2\right)^2.\)
Ebből átrendezések után, a \(\displaystyle \Delta t\)-ben csak a vezető kvadratikus rendet megtartva az
\(\displaystyle f^2+d^2-\left(d+h_2\right)^2=\left((d+h_2)a_2-fa_1\right)(\Delta t)^2\)
egyenletet kapjuk. A baloldal \(\displaystyle f\) és \(\displaystyle h_2\) definíciója miatt nulla, tehát a jobb oldal is az, azaz
\(\displaystyle a_2=\frac{f}{d+h_2}a_1=a_1\sin\varphi.\)
A két mozgásegyenlettel együtt ez három ismeretlenre három egyenlet, aminek a megoldása a kötélerőre
\(\displaystyle K_1=\frac{2(1-\sin\varphi)}{1+2\sin^2\varphi}mg=0{,}592\,mg.\)
Abban a pillanatban, amikor a rendszer a kiinduló helyzeten áthalad, a kötél nem befolyásolja a gyöngy gyorsulását, mert a kötélerőnek nincs a drót irányába eső komponense. Ilyenkor tehát \(\displaystyle a_1=-g\) és a gyöngy mozgása jó közelítéssel az
\(\displaystyle x_1=\pm v_0(\delta t)-\frac{1}{2}g(\delta t)^2\)
formában adható meg, ahol a sebesség előjele utal arra, hogy milyen irányban halad át a rendszer az adott pozíción, és \(\displaystyle \delta t\) az ettől a pillanattól mért idő. A fonálon függő test a pályája legmélyebb pontja közelében van, mozgását az
\(\displaystyle x_2=\frac{1}{2}a_2(\delta t)^2\)
kifejezés adja meg. Itt, a kötélerőt \(\displaystyle K_2\)-vel jelölve,
\(\displaystyle 2ma_2=-2mg+K_2.\)
Ilyen \(\displaystyle x_1\) és \(\displaystyle x_2\) mellett a kötél nyújthatatlanságát a
\(\displaystyle d^2+\left(\pm v_0(\delta t)-\frac{1}{2}g(\delta t)^2\right)^2=\left(d+\frac{1}{2}a_2(\delta t)^2\right)^2\)
egyenlet fejezi ki. Ebből a \(\displaystyle (\delta t)\)-ben köbös és negyedrendű tagokat elhanyagolva
\(\displaystyle a_2=\frac{v_0^2}{d}=2g\)
adódik, így
\(\displaystyle K_2=6mg.\)
Megjegyzés. Figyelemre méltó, hogy amíg a szélső helyzetben a kötél gyorsulása a gyöngy gyorsulásának a fonal irányába mutató komponense, amikor a gyöngy a kiinduló helyzeten áthalad, a gyorsulása nem, csak a sebessége befolyásolja a fonal gyorsulását. A megoldásban alkalmazott módszerrel nem nehéz belátnunk, hogy egy tetszőleges, \(\displaystyle x_1\), \(\displaystyle x_2\), \(\displaystyle v_1\), \(\displaystyle v_2\), és \(\displaystyle a_1\), \(\displaystyle a_2\) adatokkal jellemzett közbülső helyzetben
\(\displaystyle v_2=v_1\sin\phi,\qquad\textrm{és}\qquad a_2=a_1\sin\phi+\frac{\left(v_1\cos\phi\right)^2}{\sqrt{d^2+x_1^2}},\)
ahol \(\displaystyle \phi\) a fonal gyöngyhöz csatlakozó részének a vízszintessel bezárt szöge (\(\displaystyle \sin\phi=x_1/\sqrt{x_1^2+d^2}\)).
Statisztika:
19 dolgozat érkezett. 5 pontot kapott: Simon János Dániel. 4 pontot kapott: Erdélyi Dominik, Sütő Áron, Tóth Hanga Katalin. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2025. januári fizika feladatai
