 |
A P. 5624. feladat (2025. január) |
P. 5624. Két egyforma, vékony rúd egy-egy végét csukló kapcsolja össze, amely körül szabadon elfordulhatnak. Kezdetben a két rúd egy egyenes mentén helyezkedik el, az egyik rúd áll, a másik rúd szabad vége valamekkora sebességgel mozog. A rudak a súlytalanság állapotában szabadon mozoghatnak, nem hat rájuk semmilyen külső erő, és a súrlódás is elhanyagolható. Mekkora a mozgás során a két rúd által bezárt legkisebb szög?
A 2018. évi EuPhO 1. feladata nyomán
(6 pont)
A beküldési határidő 2025. február 17-én LEJÁRT.
Megoldás. Legyen az egyes rudak tömege \(\displaystyle m\), hossza \(\displaystyle \ell\) és a mozgásban lévő rúd szabad végének sebessége \(\displaystyle v\). A mozgás során a rudak mindvégig a kezdeti sebesség és a rudak kezdeti helyzete által meghatározott síkban maradnak. A két rúdból álló zárt rendszer mozgási energiája is és a perdülete is a mozgás során állandó marad.
Kezdetben az egyik (az 1. ábrán a jobb oldali) rúd tömegközéppontja \(\displaystyle v/2\) sebességgel mozog (felfelé) és \(\displaystyle v/\ell\) szögsebességgel forog, a másik rúd áll. Az egész rendszer impulzusa \(\displaystyle I=mv/2\), a rendszer tömegközéppontjának sebessége tehát \(\displaystyle v_\textrm{tkp}=I/(2m)=v/4\).
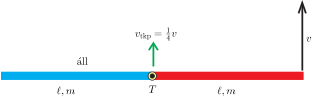
1. ábra
Térjünk át a két rúd tömegközéppontjához rögzített koordináta-rendszerre. Ebben a rendszerben a bal oldali rúd mindkét vége \(\displaystyle v/4\) sebességgel mozog lefelé és a szögsebessége nulla. A jobb oldali rúd egyik vége \(\displaystyle 3v/4\) sebességgel mozog felfelé, a másik vége \(\displaystyle v/4\) sebességgel lefelé, a szögsebessége tehát \(\displaystyle v/\ell\) (lásd a 2. ábrát).
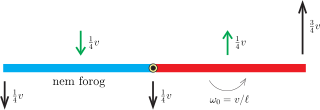
2. ábra
A rendszer mozgási energiája a tömegközépponti rendszerben
| \(\displaystyle (1)\) | \(\displaystyle E=2\cdot\frac{1}{2}m\left(\frac{v}{4}\right)^2+\frac{1}{2}\,\frac{1}{12}m\ell^2\left(\frac{v}{\ell}\right)^2=\frac{5}{48}mv^2.\) |
A rendszer perdülete (ugyancsak a tömegközépponti rendszerben)az egyes rudak saját tömegközéppontjuk körüli forgómozgásából származó ,,sajátperdületének'' és a tömegközéppontjuk mozgásából eredő ,,pályaperdületének" összege:
| \(\displaystyle (2)\) | \(\displaystyle N=0+\frac{1}{4}mv\cdot\frac{\ell}{2}+\frac{1}{12}m\ell^2\cdot\frac{v}{\ell}+\frac{1}{4}mv\cdot\frac{\ell}{2}=\frac{1}{3}mv\ell.\) |
A további mozgás során a rudak általában különböző szögsebességgel mozognak, és emiatt a közrezárt szögük időben változik. Abban a pillanatban, amikor a rudak által bezárt \(\displaystyle 2\varphi\) szög eléri a legkisebb értékét (feltételezve, hogy ilyen minimum valóban létrejön), a rudak relatív szögsebességének pillanatnyi értéke nulla kell, hogy legyen, vagyis mindkét rúd ugyanakkora \(\displaystyle \omega\) szögsebességgel fog forogni a rendszer tömegközéppontja körül (3. ábra). Azt is mondhatjuk, hogy a két rúd ebben a pillanatban merev testként viselkedik.
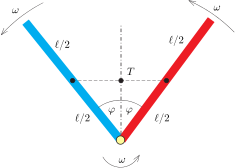
3. ábra
Legyen a két rúdból álló rendszer tehetetlenségi nyomatéka a legkisebb közrezárt szögnél a rendszer \(\displaystyle T\) tömegközéppontjára vonatkoztatva \(\displaystyle \varTheta\). Ekkor az összenergia
\(\displaystyle E=\frac{1}{2}\varTheta\omega^2,\)
az összperdület pedig
\(\displaystyle N=\varTheta\,\omega\)
módon számítható. Látszik, hogy az \(\displaystyle N^2/(2E)\) mennyiségből kiesik a szögsebesség:
| \(\displaystyle (3)\) | \(\displaystyle \frac{N^2}{2E}=\varTheta.\) |
(3) bal oldala (1) és (2)-ből adódóan
\(\displaystyle \frac{N^2}{2E}=\frac{8}{15}m\ell^2,\)
a jobb oldala pedig a Steiner-tétel felhasználásával
\(\displaystyle \varTheta=2\cdot\left[\frac{1}{12}m\ell^2+m\left(\frac{\ell}{2}\sin\varphi\right)^2\right]=\left(\frac{1}{6}+\frac {\sin^2\varphi}2\right)m\ell^2.\)
A fenti két kifejezés egyenlőségéből
\(\displaystyle \frac{8}{15}=\frac{1}{6}+\frac{\sin^2\varphi}2,\)
vagyis
\(\displaystyle \sin\varphi=\sqrt{\frac{11}{15}}\)
következik, vagyis a rudak által bezárt legkisebb szög
\(\displaystyle 2\varphi=2\arcsin\sqrt{\frac{11}{15}}\approx 118^\circ.\)
Statisztika:
11 dolgozat érkezett. 6 pontot kapott: Beke Márton Csaba, Erdélyi Dominik, Fajszi Karsa, Kovács Tamás, Tóth Hanga Katalin. 5 pontot kapott: Ujpál Bálint, Zólomy Csanád Zsolt. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2025. januári fizika feladatai
