 |
A P. 5661. feladat (2025. szeptember) |
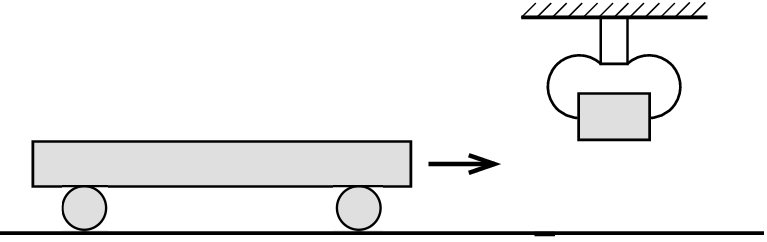
P. 5661. Egy \(\displaystyle m_1=4~\mathrm{kg}\) tömegű kiskocsi súrlódás nélkül gurul a vízszintes talajon \(\displaystyle v_1=2~\mathrm{m}/\mathrm{s}\) sebességgel. Egy \(\displaystyle m_2=1~\mathrm{kg}\) tömegű téglát egy fogószerkezet a kiskocsi későbbi útja fölött tart, épp a kiskocsi magasságában. Amikor a kocsi a szerkezet alá ér, az elengedi a téglát, ami a kocsira kerül. (Függőleges elmozdulása, és így a kocsira érés sebessége elhanyagolható.) A kocsi és a tégla között a súrlódási együttható \(\displaystyle \mu=0{,}2\). A kiskocsi elég hosszú ahhoz, hogy a tégla ne csússzon le róla.
a) Milyen közös sebességgel mozognak tovább, amikor a tégla már nem csúszik a kiskocsin?
b) Milyen hosszú úton és mennyi ideig csúszik a tégla a kiskocsin, míg ez a közös sebesség ki nem alakul?
c) A talajhoz képest melyikük mekkora utat tesz meg ezalatt?
Közli: Siposs András, Budapest
(4 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
Megoldás. A kocsira került tégla a súrlódás hatására egyenletesen gyorsul, míg a kocsi egyenletesen lassul. Ez a folyamat addig tart, ameddig a tégla és a kocsi sebessége azonossá nem válik, ettől az időponttól a két test állandó sebességgel együtt halad tovább. A kocsi \(\displaystyle a_1\) és a tégla \(\displaystyle a_2\) gyorsulását (a kiskocsi mozgásának irányát véve pozitívnak) az
$$\begin{align*} m_1a_1&=-\mu m_2g,\\ m_2a_2&=\mu m_2g \end{align*}$$egyenletek adják meg. Ezek segítségével a pillanatnyi sebességek és a talajhoz viszonyítva megtett utak (így a relatív elmozdulás is) az egyenletesen változó mozgás egyenletei alapján megadhatók, de a kérdésekben szereplő mennyiségek meghatározásához nem kell minden részletet kidolgoznunk.
a) A kialakuló \(\displaystyle v_\mathrm{k}\) közös sebességet az impulzus megmaradás törvénye alapján számoljuk ki:
\(\displaystyle v_1m_1=v_\mathrm{k}\left(m_1+m_2\right),\qquad\textrm{azaz}\qquad v_\mathrm{k}=v_1\frac{m_1}{m_1+m_2}=1{,}6\,\mathrm{m/s}.\)
b) A csúszás addig tart, amíg a tégla fel nem gyorsul erre a sebességre. Az ehhez szükséges idő
\(\displaystyle t=\frac{v_\mathrm{k}}{a_2}=\frac{v_1}{\mu g}\frac{m_1}{m_1+m_2}=0{,}82\,\mathrm{s}.\)
Ez alatt a téglának a kiskocsihoz viszonyított \(\displaystyle u\) sebessége \(\displaystyle -v_1\)-ről egyenletesen nullára változik, a relatív sebesség átlaga tehát
\(\displaystyle \overline{u}=-\frac{v_1}{2},\)
amivel az adott idő alatt
\(\displaystyle s=-\frac{v_1^2}{2\mu g}\frac{m_1}{m_1+m_2}=-0{,}82\,\mathrm{m}\)
értékkel mozdul el a platóhoz képest. (Az előjel arra utal, hogy ez az elmozdulás a kocsi mozgásával ellentétes irányú.)
c) A kiskocsi sebessége \(\displaystyle v_1\)-ről egyenletesen \(\displaystyle v_\mathrm{k}\)-ra változik, így a megtett útja
\(\displaystyle s_1=\frac{v_1+v_\mathrm{k}}{2}t=\frac{v_1^2}{2\mu g}\frac{\left(2m_1+m_2\right)m_1}{\left(m_1+m_2\right)^2}=1{,}47\,\mathrm{m}.\)
A tégla talajhoz viszonyított sebessége nulláról \(\displaystyle v_\mathrm{k}\)-ra nő, ebből a talajhoz viszonyított elmozdulása
\(\displaystyle s_2=\frac{v_\mathrm{k}}{2}t=\frac{v_1^2}{2\mu g}\left(\frac{m_1}{m_1+m_2}\right)^2=0{,}65\,\mathrm{m}.\)
Statisztika:
67 dolgozat érkezett. 4 pontot kapott: Blaskovics Ádám, Csáki Anikó, Elekes Panni, Fuchs Vince, Gyenes Károly, Hajdu Eszter, Halmosi Dávid, Kirst Alexander, Kossár Benedek Balázs, Kovács Tamás , Mezei Marcell, Misik Balázs, Molnár Lili, Monori Bence, Murányi Nimród Máté, Nagy Gellért Ákos, Nguyen Thien Minh , Papp Emese Petra, Poczai Dorottya, Ruzsics Gréta, Sipeki Andor, Steller Judit, Szimeiszter Dávid, Tóth Hanga Katalin, Winhoffer Júlia, Wolf Erik. 3 pontot kapott: Békési Máté, Bertollo Antonio, Bús László Teodor, Erdélyi Dominik, Ferencz Kevin, Gilyán Zsombor, Gombos Domokos-Adrián, Horváth Péter, Illés Dóra, Kirschner Bálint, Kocsán Bence János, Kovács Dániel, Kovács Tamás, Mi Feiyu, Ruzsicska Soma, Szkalák Álmos, Tasnádi Zsófia, Vértesi Janka, Zhao Aaron . 2 pontot kapott: 13 versenyző. 1 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2025. szeptemberi fizika feladatai

