 |
A P. 5663. feladat (2025. szeptember) |
P. 5663. Az ábrán látható rendszer egyensúlyban van. A 45 kg tömegű merevítő rúd végére 225 kg tömegű terhelést akasztottak.
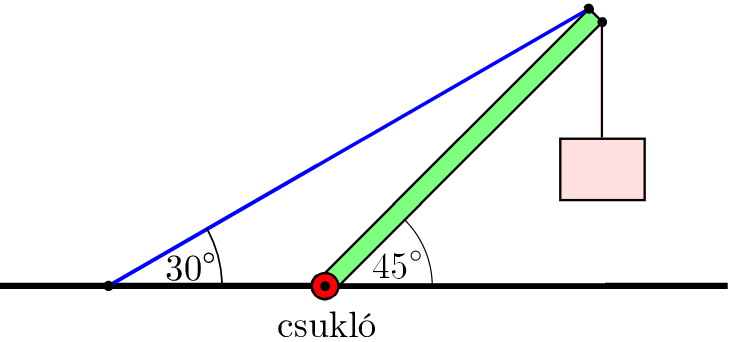
Határozzuk meg a feszítőkábelben ébredő erőt és a csukló által a merevítő rúdra ható erő nagyságát és irányát!
Példatári feladat
(4 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
Megoldás. Legyen a merevítő rúd hossza \(\displaystyle \ell\), tömege \(\displaystyle m=45\,\mathrm{kg}\) és a terhelés tömege \(\displaystyle M=225\,\mathrm{kg}\), a feszítőkábelben ébredő erő \(\displaystyle T\). Vegyük észre, hogy a merevítőrúd és a feszítőkábel által bezárt szög \(\displaystyle \alpha=15^\circ\). A következő ábrán néhány erőhöz tartozó erőkart olvashatjuk le a csuklóhoz mint forgástengelyhez viszonyítva.
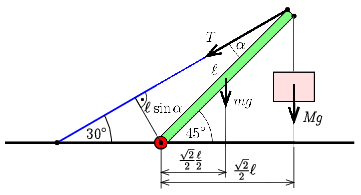
Írjuk fel a csuklóra a forgatónyomatékok egyensúlyát:
\(\displaystyle Mg\frac{\sqrt{2}}{2}\ell+mg\frac{\sqrt{2}}{2}\frac{\ell}{2}=T\ell\sin\alpha.\)
Az adatokat behelyettesítve:
\(\displaystyle T=6{,}63\,\mathrm{kN}.\)
A továbbiakban az erők egyensúlyával számolunk. A feszítőkábel a függőlegessel \(\displaystyle 60^\circ\)-os szöget zár be, ezért a kábelben ébredő erő függőleges összetevője \(\displaystyle T/2\). Ehhez még hozzá kell adni a rúd és a terhelés súlyát, hogy megkapjuk a csukló által a rúdra ható erő függőleges összetevőjét:
\(\displaystyle F_y=\frac{T}{2}+(m+M)g=5{,}97\,\mathrm{kN}.\)
A vízszintes összetevő megegyezik a kábelben ható erő vízszintes komponensével:
\(\displaystyle F_x=\frac{\sqrt{3}}{2}T=5{,}74\,\mathrm{kN}.\)
A csuklóban ébredő erő nagysága:
\(\displaystyle \sqrt{F_x^2+F_y^2}=8{,}28\,\mathrm{kN},\)
és ez az erő a terhelés felé hajlik, a függőlegessel bezárt szöge:
\(\displaystyle \arctg\left({\frac{F_x}{F_y}}\right)=43{,}9^\circ.\)
Statisztika:
51 dolgozat érkezett. 4 pontot kapott: Békési Máté, Bense Tamás, Bús László Teodor, Erdélyi Dominik, Fuchs Vince, Illés Dóra, Kirst Alexander, Kossár Benedek Balázs, Mi Feiyu, Molnár Lili, Monori Bence, Papp Emese Petra, Rajtik Sándor Barnabás, Simon János Dániel, Szécsi Bence, Tasnádi Zsófia, Török Tibor, Vértesi Janka, Vigh István Csaba, Winhoffer Júlia, Zádori Gellért. 3 pontot kapott: Bertollo Antonio, Gilyán Zsombor, Halmosi Dávid, Kovács Dániel, Mezei Marcell, Nagy Gellért Ákos, Ruzsics Gréta, Vincze Anna, Zhao Aaron . 2 pontot kapott: 9 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2025. szeptemberi fizika feladatai

