 |
A P. 5666. feladat (2025. szeptember) |
P. 5666. Egy \(\displaystyle U_0\) feszültségen lévő síkkondenzátor lemezeinek töltését megváltoztatjuk. A pozitív lemez töltését háromszorosára növeljük, a negatívét felére csökkentjük. Mekkora lesz a lemezek között a feszültség?
Közli: Wiedemann László, Budapest
(4 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
I. megoldás. Szokásos körülmények között a kondenzátor két lemezének össztöltése nulla. Ha a kondenzátor kapacitása \(\displaystyle C\) és a lemezek közötti feszültség \(\displaystyle U_0\), akkor a lemezek töltése \(\displaystyle Q_0=CU_0\). Az 1. ábra vázlatosan mutatja a kialakuló elektrosztatikus mezőt. (Ha a lemezek nagyon közel vannak egymáshoz, a széleffektusokat és a szórt elektromos teret elhanyagolhatjuk, de ezt a közelítést az alábbiakban nem fogjuk használni.)
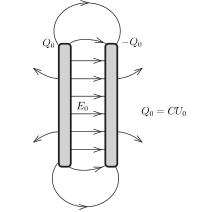
1. ábra
Tekintsük most azt az állapotot, amelyben mindkét lemezen azonos előjelű és ugyanakkora \(\displaystyle Q^*\) nagyságú töltés található (2. ábra). Ezek a töltések az egyensúlyi állapotban főleg a lemezek külső oldalán helyezkednek el, de nem egyenletes eloszlásban, hanem a lemez széleihez közeledve egyre sűrűbben, és a lemezek közötti térrészben is lehet valamilyen elektromos mező.
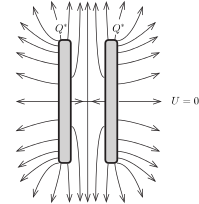
2. ábra
Az egész mező pontos alakját nem ismerjük (szerencsére nincs is szükségünk erre), de azt biztosan állíthatjuk, hogy a lemezek felezősíkjára nézve tükörszimmetrikus. Emiatt a két lemez potenciálja ugyanakkora, a lemezek között nem alakul ki feszültség.
A szuperpozíció elve szerint, ha valamilyen elrendezésben a töltések egyensúlyban vannak a fémfelületeken, akkor valamennyi töltést arányosan (mondjuk \(\displaystyle \lambda\)-szorsára) megnövelve ismét egyensúlyi elrendezést kapunk, amelyben a térerősségek és a potenciálkülönbségek mindenhol az eredeti értékek \(\displaystyle \lambda\)-szorosai. Továbbá az is igaz, hogy két egyensúlyi töltéselrendezést összeadva ismét egyensúlyi töltéselrendezést kapunk, és ebben a térerősségek, illetve a potenciálok bármely helyen az ottani eredeti értékek vektori, illetve skalár összegei.
Nevezzük az 1. ábrán látható töltéselrendezést 1-esnek, a 2. ábrán láthatót pedig 2-esnek. Képezzük ezek után az 1-es állapot \(\displaystyle \lambda\)-szorosának és a 2-es állapotnak a szuperpozícióját, és válasszuk \(\displaystyle \lambda\)-t és \(\displaystyle Q^*\)-t úgy, hogy a szuperpozíció után a lemezek töltése a feladat szövegében megadott érték legyen (3. ábra).
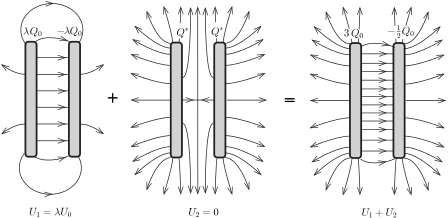
3. ábra
Fennáll tehát:
| \(\displaystyle (1)\) | \(\displaystyle \lambda Q_0+Q^*=3Q_0,\) |
| \(\displaystyle (2)\) | \(\displaystyle -\lambda Q_0+Q^*=-\frac12Q_0.\) |
Az (1) egyenletből (2)-t kivonva kapjuk, hogy
\(\displaystyle 2\lambda Q_0=\left(3+\frac12\right)Q_0,\)
vagyis \(\displaystyle \lambda=\frac{7}{4}\). A potenciálkülönbségek szuperpozíciója, vagyis a keresett feszültség:
\(\displaystyle U=U_1+U_2=\lambda\,U_0+0=\frac{7}{4}\,U_0.\)
Megjegyzés. A szuperpozíció elvének alkalmazásakor lényeges, hogy a fémfelületek a szuperpozíció minden tagjánál ugyanott helyezkedjenek el, és a töltések rajtuk egyensúlyi állapotban legyenek. Sok tankönyvben szerepel az a hibás ábra, amelyben egy síkkondenzátor elektrosztatikus terét egy-egy magában álló pozitív és negatív töltésű fémlap (homogénnek tekintett) erőterének összegeként próbálják előállítani. Ez két ok miatt is hibás! Egyrészt egyetlen feltöltött lemez elektromos tere a lemez két oldalán még a lemez közvetlen közelében sem homogén, hanem a 2. ábrán láthatóhoz hasonló, ha a lemezek távolságát nullára csökkentjük. Másrészt ebben az elrendezésben a ,,szuperpozíció'' két tagjában és az eredményben nem ugyanazok a fémlemezek vesznek részt, sőt még a darabszámuk is eltér egymástól.
II. megoldás. Ha az egyik (1-es jelű) lemezt Q=1 egységnyi töltéssel látjuk el, akkor a potenciálja valamekkora \(\displaystyle x\) értékre nő, a másik lemez potenciálja pedig valamekkora \(\displaystyle y\) lesz. (\(\displaystyle x\) és \(\displaystyle y\) nagysága a lemezek geometriai adataiból és a távolságukból elvben kiszámítható, de a konkrét értékükre a továbbiakban nem lesz szükségünk.) Ha csak a 2. lemezt töltjük fel egységnyi töltéssel, akkor a szerepek megcserélődnek, az 1. lemez potenciálja lesz \(\displaystyle y\), és a \(\displaystyle 2.\) lemezé \(\displaystyle x\) (4. ábra).

4. ábra
Ha a lemezeket nagyobb töltéssel látjuk el, a potenciálok is arányosan nagyobbak lesznek, és ha mindkét lemezen vannak töltések, a potenciálok összeadódnak. Ez a szuperpozíció elvvel egyenértékű, de annak a korábbiakban leírttól kicsit eltérő megfogalmazása. Több elektromosan töltött fémfelületnél a potenciálok és töltések kapcsolatáról (az ú.n. kapacitásmátrixról) további érdekességek olvashatók a KöMaL 2019. évi októberi számában megjelent cikkben (Woynarovich Ferenc: Kapacitások összetett rendszerekben).
A szokásos, \(\displaystyle \pm Q_0\) töltésű kondenzátor lemezeinek potenciálja (5. ábra)
\(\displaystyle \Phi_1=xQ_0-yQ_0\qquad\textrm{és}\qquad\Phi_2=yQ_0-xQ_0,\)
a lemezek közötti potenciálkülönbség (a kondenzátor feszültsége)
\(\displaystyle U_0=\Phi_1-\Phi_2=2(x-y)Q_0.\)

5. ábra
Ha most az 1. lemez töltését \(\displaystyle 3\,Q_0\)-ra növeljük, a másikét pedig \(\displaystyle -\tfrac{1}{2}Q_0\)-ra változtatjuk (6. ábra), akkor a lemezek potenciálja:
\(\displaystyle \Phi_1'=3xQ_0-\frac{1}{2}yQ_0\qquad\textrm{és}\qquad\Phi_2'=-\frac{1}{2}xQ_0+3yQ_0,\)
a lemezek közötti potenciálkülönbség (a kondenzátor feszültsége)
\(\displaystyle U=\Phi_1'-\Phi_2'=\frac{7}{2}(x-y)Q_0=\frac{7}{2}\cdot\frac{U_0}{2}=\frac{7}{4}U_0.\)
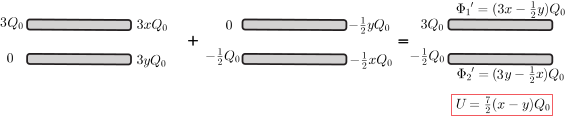
6. ábra
A fémlemezek közötti feszültség tehát az eredeti érték \(\displaystyle \frac{7}{4}\)-szerese lesz. Ez az eredmény nem csak az elhanyagolható szórt terű síkkondenzátorokra érvényes, hanem bármilyen alakú és tetszőleges távolságú fémdarabokra is igaz.
Statisztika:
33 dolgozat érkezett. 4 pontot kapott: Bélteki Teó, Csáki Anikó, Elekes Panni, Erdélyi Dominik, Gyenes Károly, Hornyák Zalán Zétény, Kossár Benedek Balázs, Kovács Tamás , Misik Balázs, Simon János Dániel, Sipeki Andor, Szécsi Bence, Tajta Sára, Tasnádi Zsófia, Tóth Hanga Katalin, Török Tibor, Vigh István Csaba, Zádori Gellért. 3 pontot kapott: Chen Yu, Kirst Alexander, Papp Emese Petra. 2 pontot kapott: 3 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2025. szeptemberi fizika feladatai

