 |
A P. 5667. feladat (2025. szeptember) |
P. 5667. Az ábrán egy izzólámpa látható két homorú tükör között. A jobb oldali tükör párhuzamos fénynyalábot állít elő, míg a bal oldali, kis méretű tükör megakadályozza, hogy az izzólámpa fényének jelentős része kiszökjön ebből az összeállításból, ami egy gépkocsi reflektorának felel meg.
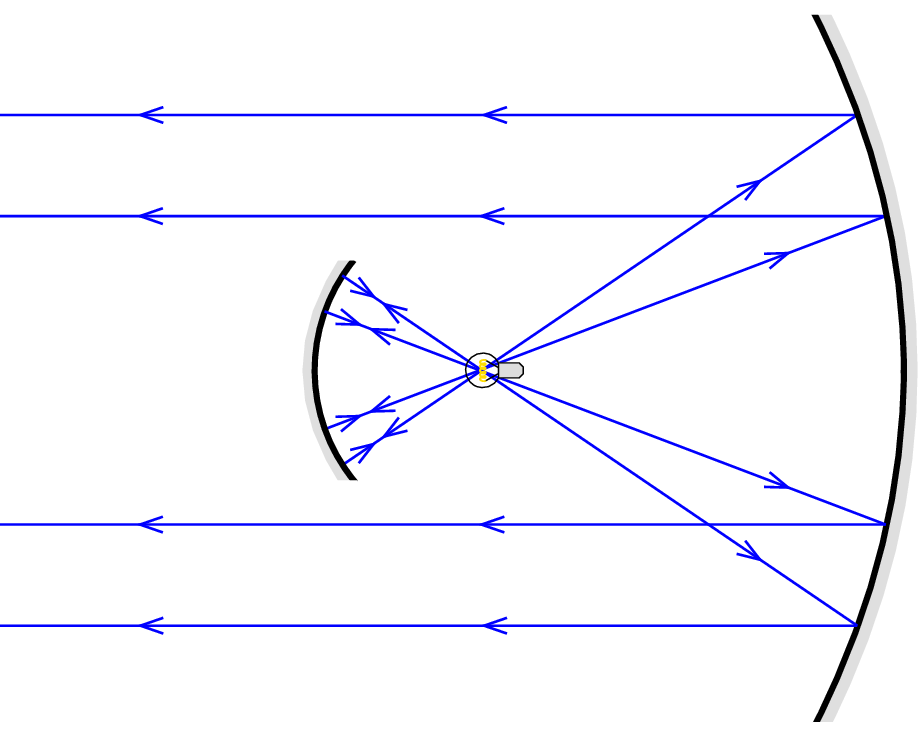
a) Magyarázzuk el, hogy miért ad erősebb fényt a reflektor a bal oldali kis tükör használatával, mint nélküle!
b) Vonalzóval végezzünk méréseket az ábrán, és állapítsuk meg a két tükör fókusztávolságának arányát!
c) Vonalzóval elvégzett méréseink alapján becsüljük meg, hogy az izzólámpa fényének hány százaléka kerül a reflektor által előállított párhuzamos fénynyalábba a kis tükör használata nélkül, illetve a kis tükör beépítésével!
Példatári feladat nyomán
(5 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
Megoldás. a) A kis tükör a lámpa előre szóródó fényéből jelentős hányadot visszaver, és így ez a fény is bekerül a reflektor által létrehozott fénynyalábba. Ez annak ellenére növeli a reflektor teljesítményét, hogy a kis tükör bizonyos hányadot kitakar a párhuzamos fénynyalábból.
b) A kis tükör megfordítja a fénysugarakat, vagyis a lámpa izzószála a gömbtükör geometriai középpontjában van. Így közvetlenül lemérhetjük a kis tükör felületének görbületi sugarát, és ennek fele adja jó közelítéssel a kis tükör fókusztávolságát. A nagy tükör forgási paraboloid, aminek fókuszában van a lámpa izzószála. Kinyomtatott ábrán elvégzett mérések szerint a nagy tükör fókusztávolsága körülbelül 2,5-szerese a gömbtükör sugarának, vagyis a fókusztávolságok aránya körülbelül 5.
c) A számszerű eredményhez használnunk kell a térszög fogalmát, aminek a mértékegysége a szteradián (sr). A teljes térszög \(\displaystyle 4\pi\,\mathrm{sr}\), mert az egységsugarú gömb felülete \(\displaystyle 4\pi\). Másképp fogalmazva a térszöget úgy kaphatjuk meg, hogy egy \(\displaystyle r\) sugarú gömb felületén kijelöljük a vizsgált térszögnek megfelelő területet, és ezt elosztjuk \(\displaystyle r^2\)-tel. Megmutatható, hogy amennyiben egy egyenes kúp által kimetszett felületről van szó, amikor a kúp csúcsa a gömb középpontjában van (ez a leggyakoribb eset), és a kúp félnyílásszöge \(\displaystyle \varphi\), akkor a kérdéses térszög: \(\displaystyle \Omega=2\pi(1-\cos{\varphi})\). Az ábrán az eredeti ábrát speciális sugarakkal kiegészítettük, és bejelöltünk három félnyílásszöget.
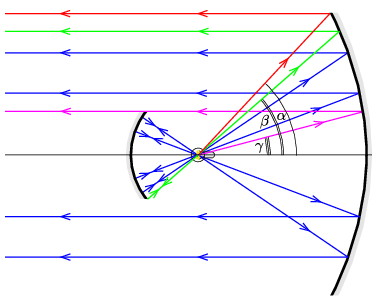
Ha nem használnánk a kis tükröt, akkor a parabolatükör az \(\displaystyle \alpha\) félnyílásszögű kúpból érkező sugarakat alakítaná párhuzamos nyalábbá. A kinyomtatott ábrán szögmérővel elvégzett mérések szerint \(\displaystyle \alpha=47^\circ\). Az ehhez tartozó térszög:
\(\displaystyle \Omega_1=2\pi(1-\cos\alpha)=2{,}00\,\mathrm{sr}.\)
Ilyenkor az izzólámpa fényének \(\displaystyle \tfrac{2{,}00}{4\pi}=0{,}159\approx 16\%\)-a kerül be a párhuzamos fénynyalábba.
A kis tükör használatával az előre szóródó fényből \(\displaystyle \beta\) térszöggel verődik vissza fény, ami szintén bekerül a párhuzamos nyalábba. Azonban az \(\displaystyle \alpha\) és a \(\displaystyle \beta\) térszögű sugarakból a nagy tükörről történő visszaverődés után a kis tükör a \(\displaystyle \gamma\) térszöghöz tartozó részt kitakarja. A mérések szerint \(\displaystyle \beta=42^\circ\) és \(\displaystyle \gamma=15^\circ\). A kérdéses térszögeket (melyek megadják a nyalábba kerülő fény arányát) így számíthatjuk ki:
$$\begin{align*} \Omega_2&=(2\pi(1-\cos\alpha)-2\pi(1-\cos\gamma))+(2\pi(1-\cos\beta)-2\pi(1-\cos\gamma))=\\ &=2\pi(2\cos\gamma-(\cos\alpha+\cos\beta))=3{,}18\,\mathrm{sr}. \end{align*}$$A kis tükör segítségével az izzólámpa fényének \(\displaystyle \tfrac{3{,}18}{4\pi}=0{,}253\approx 25\%\)-a kerül be a reflektor nyalábjába.
Láthatjuk tehát, hogy a kis tükör több mint másfélszeresére növeli a reflektor fényerejét.
Megjegyzés. A fényből az izzó foglalata is kitakar valamennyit, de ezt nem vettük figyelembe a számításnál. A kis tükröt gyakran beleépítik az izzóba.
Statisztika:
27 dolgozat érkezett. 5 pontot kapott: Bélteki Teó, Bús László Teodor, Sümeghi Nándor . 4 pontot kapott: Beke Márton Csaba, Kovács Tamás, Ruzsics Gréta, Tajta Sára. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2025. szeptemberi fizika feladatai

