 |
A P. 5669. feladat (2025. szeptember) |
P. 5669. Egy \(\displaystyle R=5~\mathrm{cm}\) sugarú, \(\displaystyle m=0{,}5~\mathrm{kg}\) tömegű, homogén anyageloszlású tárcsa \(\displaystyle r=0{,}5~\mathrm{cm}\) sugarú tengelyéhez egy \(\displaystyle L=20~\mathrm{cm}\) hosszúságú, vékony fonál egyik végét rögzítjük, és a fonál \(\displaystyle L/2\) hosszúságú részét a tengelyre feltekerjük. A függőleges fonál másik végét rögzített helyzetben tartva a tárcsát elengedjük.
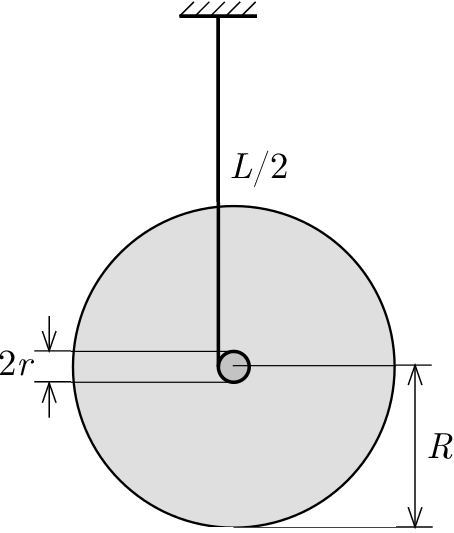
a) Mekkora erő feszíti a fonalat az egyenletesen gyorsuló tárcsa (,,jojó'') mozgása közben?
b) Mekkora a tárcsa tengelyének sebessége a fonál kitekeredésének pillanatában?
c) A tárcsa függőleges mozgásának megfordulásakor a fonalat feszítő erő egy rövid időre megnő (a tárcsa ,,ránt egyet'' a fonálon). Becsüljük meg a fonálerő átlagos értékét a rántás alatt!
A tengely tömegét, a fonál függőlegestől való eltérését és a közegellenállást elhanyagolhatjuk. A tárcsa szögsebességét az ,,átfordulás'' alatt tekintsük állandónak.
Közli: Gnädig Péter, Vácduka
(6 pont)
A beküldési határidő 2025. október 15-én LEJÁRT.
Megoldás. A feladat a jojó nevű játékot modellezi. Várható például, hogy a kicsi \(\displaystyle \tfrac{r}{R}\) arány miatt a korong tömegközéppontja a kerületi sebességéhez képest lassan fog mozogni.
a) A fonalat feszítő erőt jelöljük \(\displaystyle F\)-fel, a korong tömegközéppontjának gyorsulását \(\displaystyle a\)-val. A korong tömegközéppontjára írjuk fel a mozgásegyenletet:
| \(\displaystyle (1)\) | \(\displaystyle ma=mg-F,\) |
A korong eközben a feltekert cérna miatti kényszerfeltétel következtéen \(\displaystyle \beta=\frac{a}{r}\) szöggyorsulással felpörög, amire a forgásegyenlet:
\(\displaystyle \Theta\beta=rF,\)
ahol a korong tehetetlenségi nyomatéka \(\displaystyle \Theta=\tfrac{1}{2}mR^2\). Behelyettesítve \(\displaystyle \Theta\)-t és \(\displaystyle \beta\)-t:
\(\displaystyle \frac{1}{2}mR^2\frac{a}{r}=rF.\)
Ebből fejezzük ki \(\displaystyle ma\)-t:
\(\displaystyle ma=2\left(\frac{r}{R}\right)^2F.\)
Ezt visszahelyettesítve az (1) egyenletbe megkapjuk a kötelet feszítő erőt:
\(\displaystyle F=\frac{mg}{1+2\left(\frac{r}{R}\right)^2}=4{,}8\,\mathrm{N}.\)
b) A tárcsa tömegközéppontjának \(\displaystyle v\) sebességét az energiamegnaradásból fogjuk meghatározni. A fonál teljes kitekeredésekor a korong helyzeti energiája \(\displaystyle \tfrac{1}{2}Lmg\)-vel csökken a induláshoz képest. Ez alakul a korong \(\displaystyle \tfrac{1}{2}mv^2\) tömegközépponti mozgási, és \(\displaystyle \tfrac{1}{2}\Theta\omega^2=\tfrac{1}{2}\Theta\left(\tfrac{v}{r}\right)^2\) forgási energiájává:
\(\displaystyle \frac{1}{2}Lmg=\frac{1}{2}mv^2+\frac{1}{2}\Theta\left(\frac{v}{r}\right)^2.\)
Behelyettesítve \(\displaystyle \Theta=\tfrac{1}{2}mR^2\)-t és egyszerűsítve \(\displaystyle \tfrac{1}{2}m\)-mel:
\(\displaystyle Lg=v^2\left(1+\frac{1}{2}\left(\frac{R}{r}\right)^2\right).\)
Ebből a sebesség:
\(\displaystyle v=\frac{r}{R}\sqrt{\frac{2Lg}{1+2\left(\frac{r}{R}\right)^2}}=0{,}196\,\mathrm{\frac{m}{s}}.\)
c) Fordulásakor a korong lendülete \(\displaystyle \Delta p=2mv\) értékkel változik. Közben a korong jó közelítéssel \(\displaystyle \omega=\frac{v}{r}\) szögsebességgel forog, így a félfordulat megtétele \(\displaystyle \Delta t=\tfrac{\pi}{\omega}=\tfrac{\pi r}{v}\) ideig tart. Az átlagos fonálerő, a korong súlyával együtt:
\(\displaystyle F_f=mg+\frac{\Delta p}{\Delta t}=mg+\frac{2mv^2}{\pi r}.\)
Mivel a feladat csak becslést kér, \(\displaystyle v\) behelyettesítésénél a \(\displaystyle \left(\tfrac{r}{R}\right)^2=10^{-2}\) nagyságrendű korrekciót elhanyagoljuk:
\(\displaystyle F_f\approx mg\left(1+\frac{4Lr}{\pi R^2}\right)=7{,}4\,\mathrm{N}.\)
Statisztika:
36 dolgozat érkezett. 6 pontot kapott: Beke Márton Csaba, Bélteki Teó, Erdélyi Dominik, Gyenes Károly, Kossár Benedek Balázs, Papp Emese Petra, Sümeghi Nándor , Szécsi Bence, Török Tibor, Vigh István Csaba. 5 pontot kapott: Hornyák Zalán Zétény, Kirst Alexander, Kovács Tamás, Murányi Nimród Máté, Vértesi Janka, Zólomy Csanád Zsolt. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2025. szeptemberi fizika feladatai

